PLDI '21 Talk Transcription: AKG: Automatic Kernel Generation for Neural Processing Units using Polyhedral Transformation
Jie Zhao, Bojie Li, Wang Nie, Zhen Geng, Renwei Zhang, Xiong Gao, Bin Cheng, Chen Wu, Yun Cheng, Zheng Li, Peng Di, Kun Zhang, Xuefeng Jin. AKG: Automatic Kernel Generation for Neural Processing Units using Polyhedral Transformations. 42nd ACM SIGPLAN International Conference on Programming Language Design and Implementation (PLDI’21). Virtual, Canada, June 20-25, 2021. pp.1233-1248. [Paper PDF] [Slides by Jie Zhao]

Hello everyone, I’m Jie Zhao. In this talk, I will introduce our work on automated kernel generation for NPUs using polyhedral transformations. This is a collaborative work between the Static Laboratory of Mathematical Engineering, Advanced Computing, and Huawei Technologies.

The presentation is composed of the following content. Let’s start with the introduction.
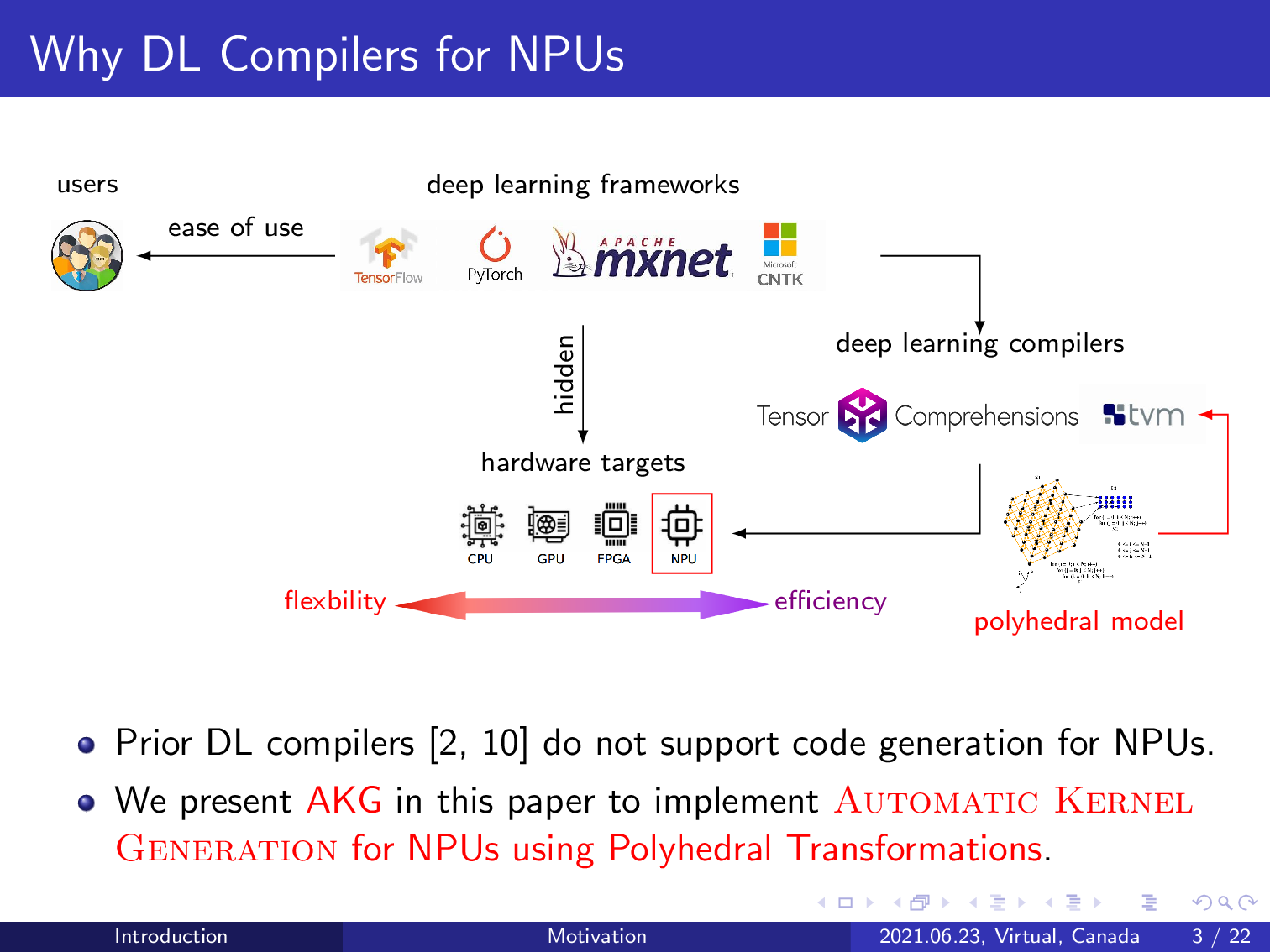
Existing deep learning frameworks like TensorFlow, PyTorch, MXNet, and CNTK provide ease-of-use interfaces to their users by hiding the underlying architectural details of the targets. However, these frameworks fall short in supporting custom operators invented by users or algorithm engineers. To address this issue, researchers from the compiler community developed deep learning compilers like Tensor Comprehensions and TVM.
These deep learning compilers have shown their effectiveness on multiple devices, including CPU, GPU, and FPGA. But these deep learning compilers rarely support code generation for NPUs due to their complex memory hierarchy. A dedicated NPU generally exhibits stronger computing power than the widely used targets supported by existing works. We present AKG in this paper to implement kernel generation for an NPU by integrating the polyhedral model into the TVM compiler.
The content you provided is already in English, so according to your instructions, I will output it as-is without translation:
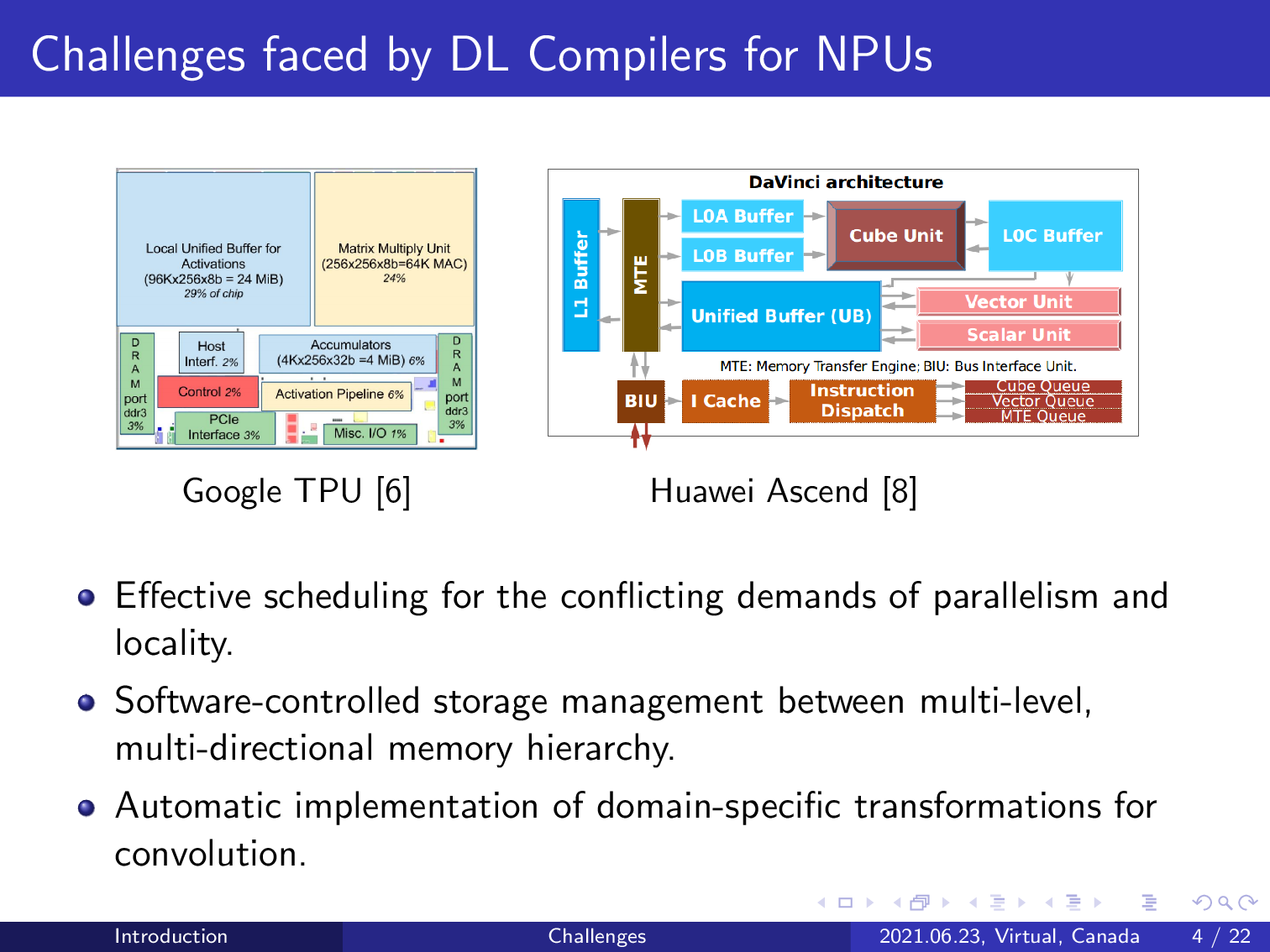
However, designing deep learning compilers for NPUs also has to address the challenges posed by the complex memory hierarchy of modern accelerators. For example, here we show the flow plan of a Google TPU. Unlike the traditional memory hierarchy pyramid, these accelerators also exhibit multi-level, multi-directional memory systems.
As a result, the required deep learning compilers have to be able to do effective scheduling for the conflicting demands of parallelism and latency, manage the complex memory hierarchy in a software-controlled manner, and automatically implement domain-specific transformations to fit the different compute units. We address all of these challenges using AKG.
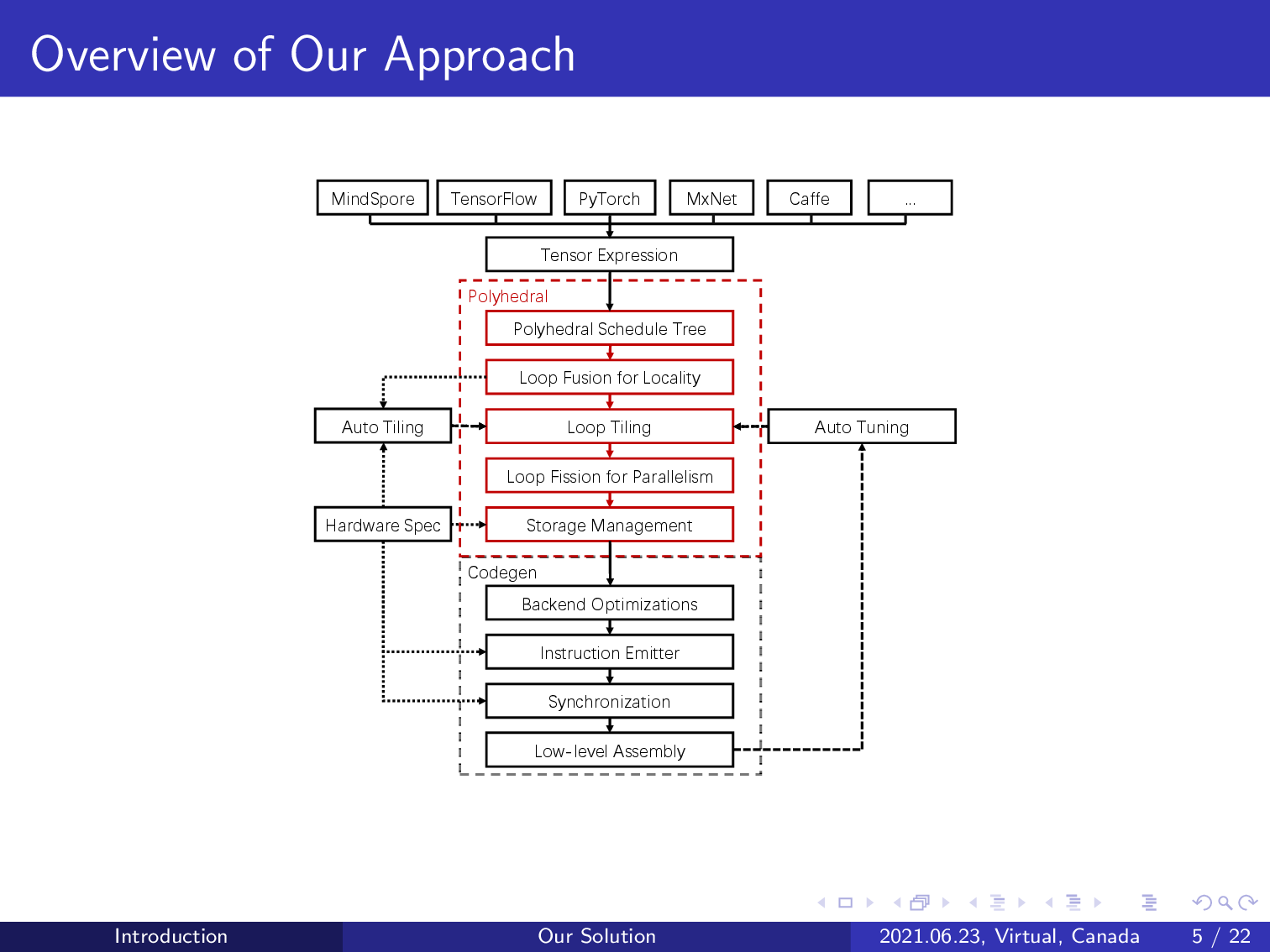
This is the architecture of our approach.
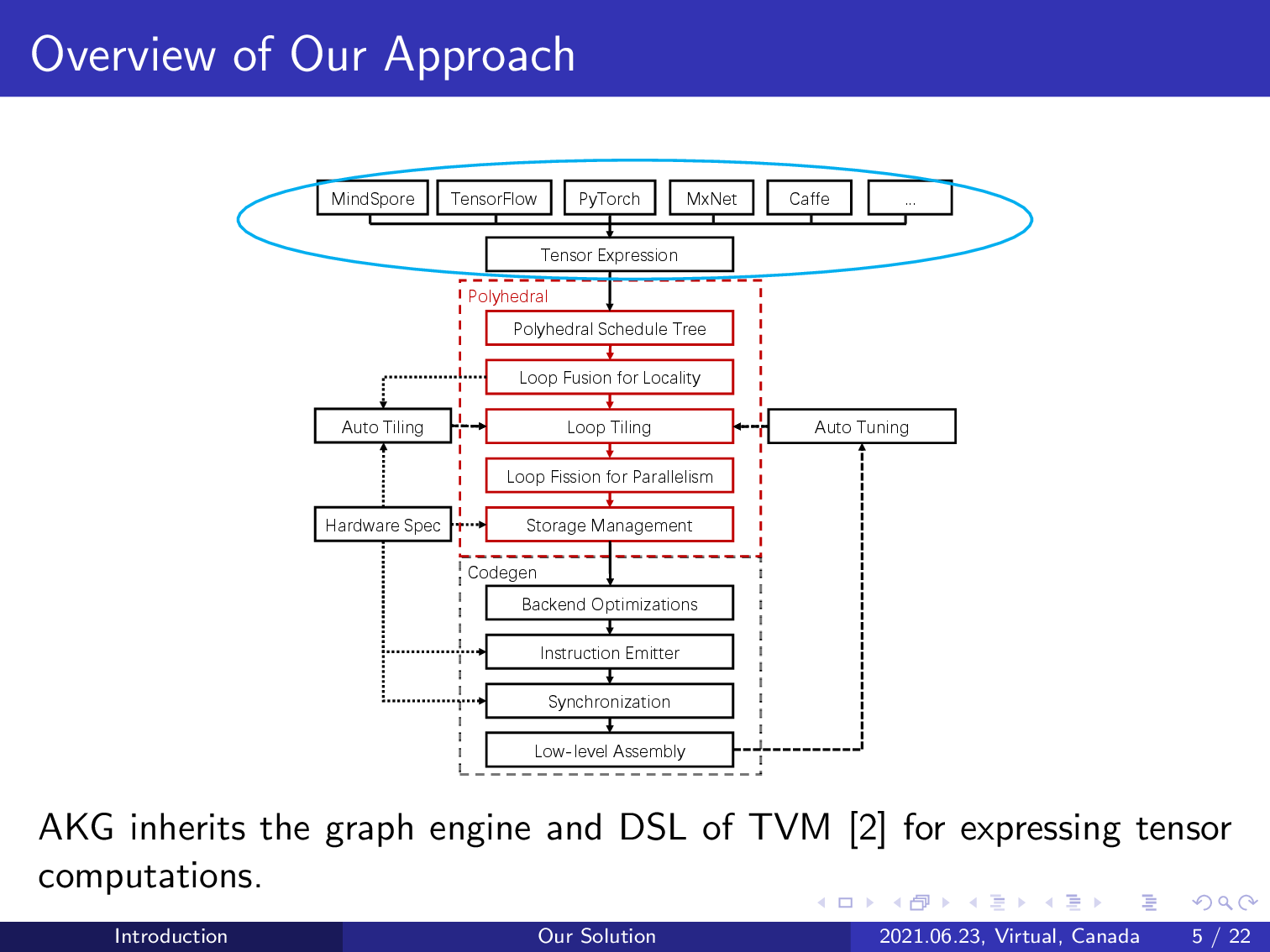
Our compiler integrates with the graph engine of TVM and reuses its DSL to express tensor computations. The compilation workflow can support various deep learning frameworks.
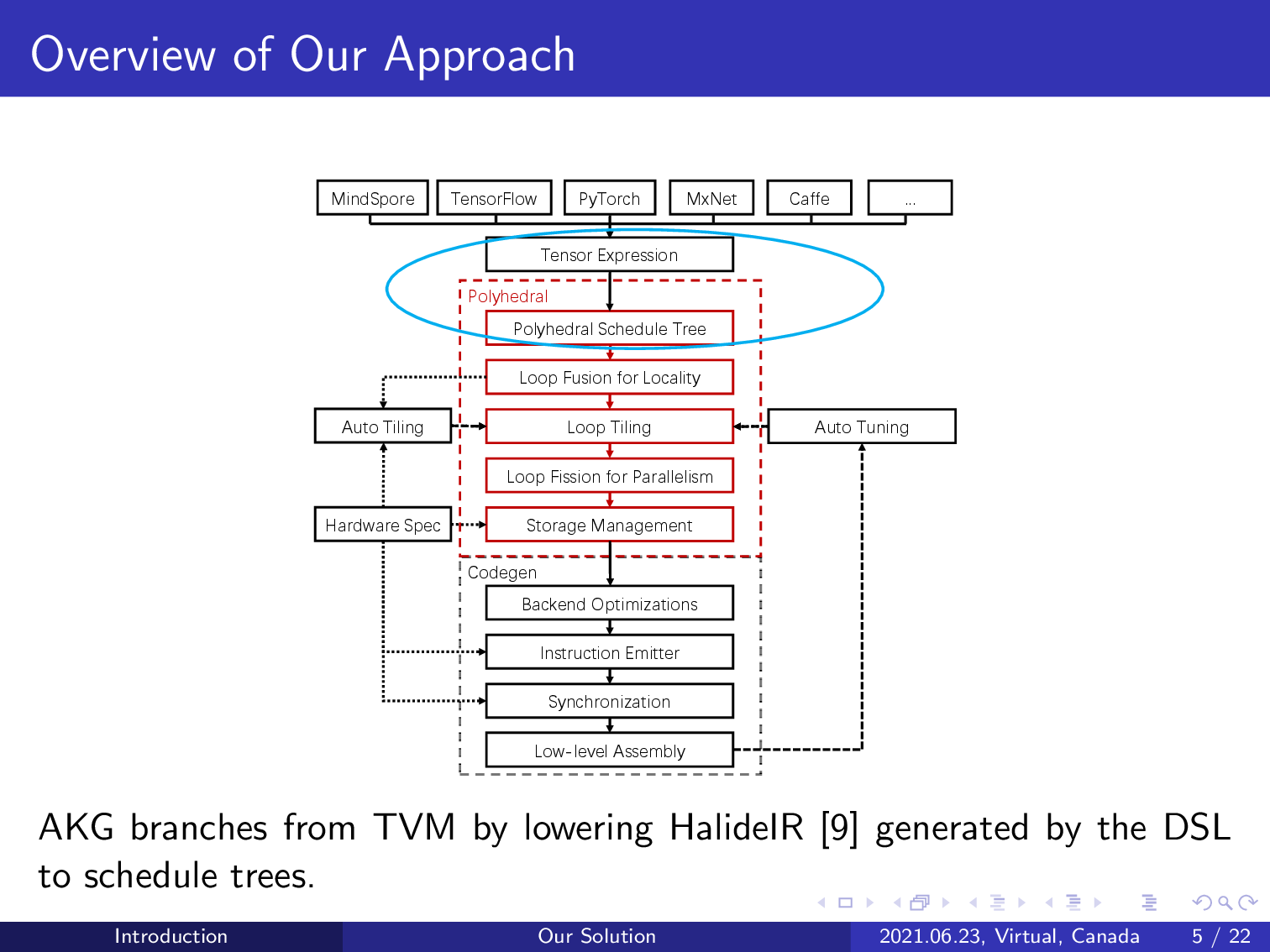
AKG branches from TVM by lowering its intermediate representation to a polyhedral representation schedule tree. The polyhedral model can be introduced to perform various compositions of loop transformations given an initial schedule tree representation.
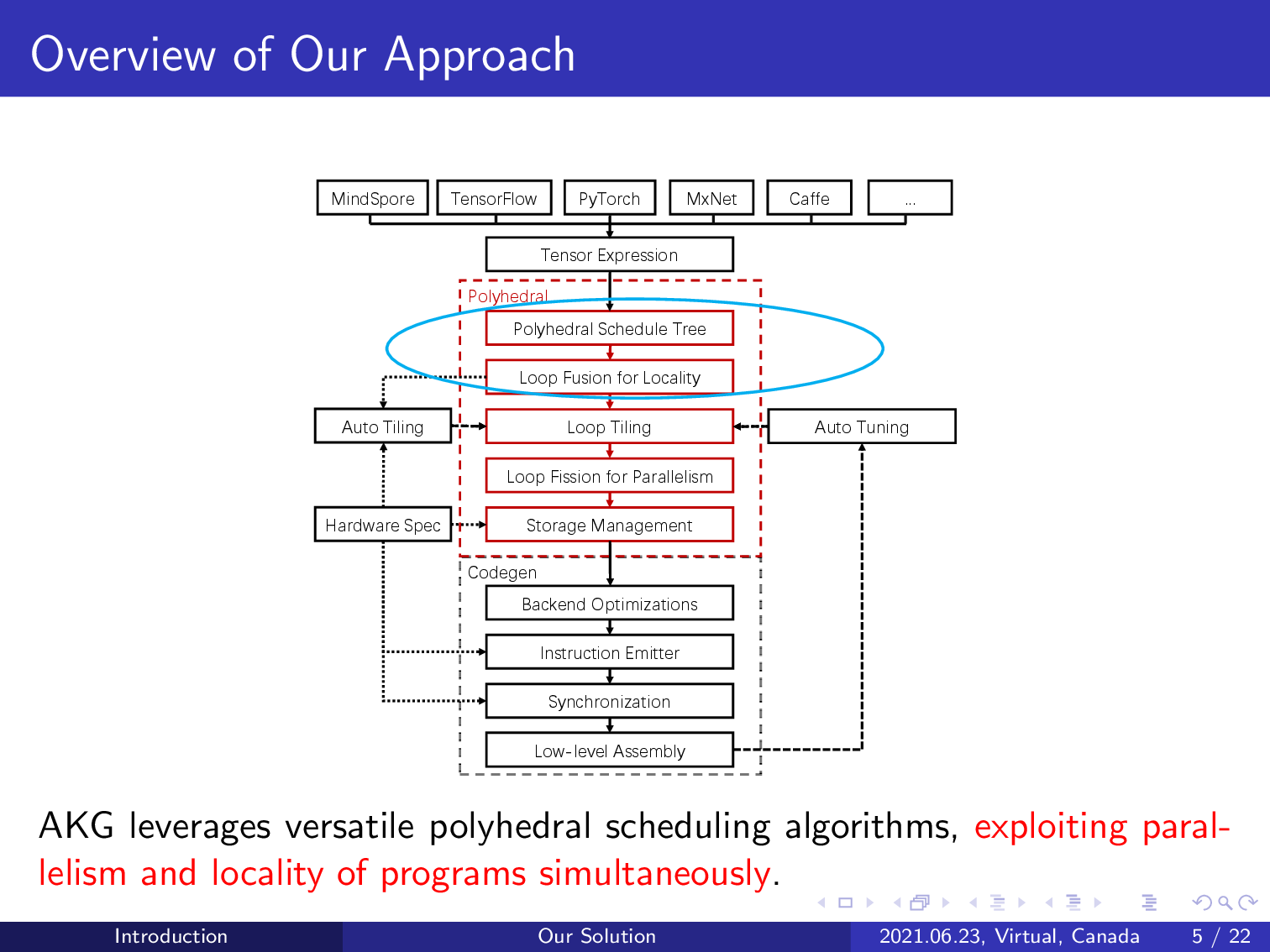
AKG first uses the integer linear programming-based schedulers of the polyhedral model to exploit both parallelism and data locality, avoiding the need for manual schedule specification.
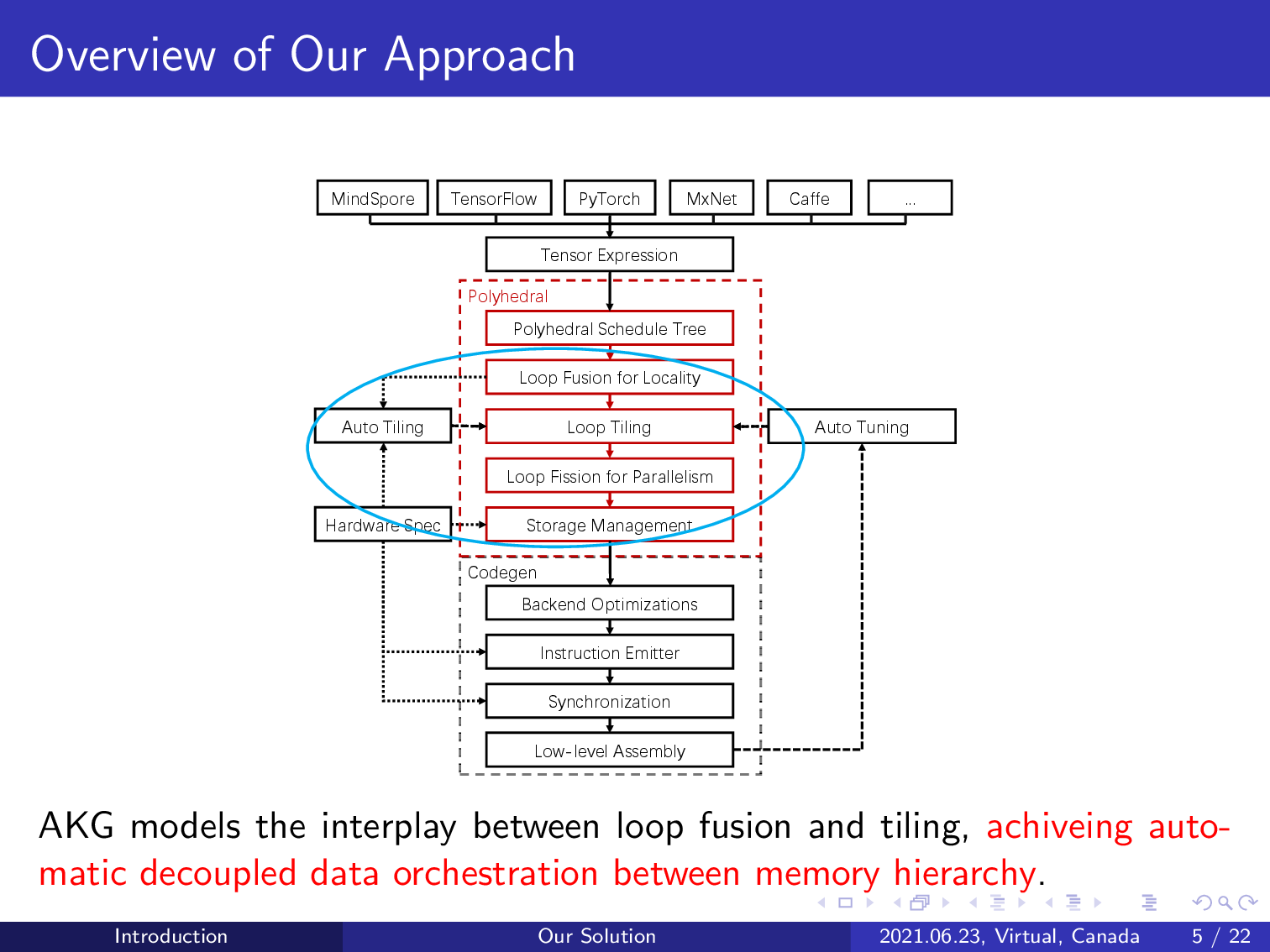
It also models the interplay between loop tiling and fusion, achieving automatic handling of data orchestration on the multi-level, multi-directional memory hierarchy of an NPU.
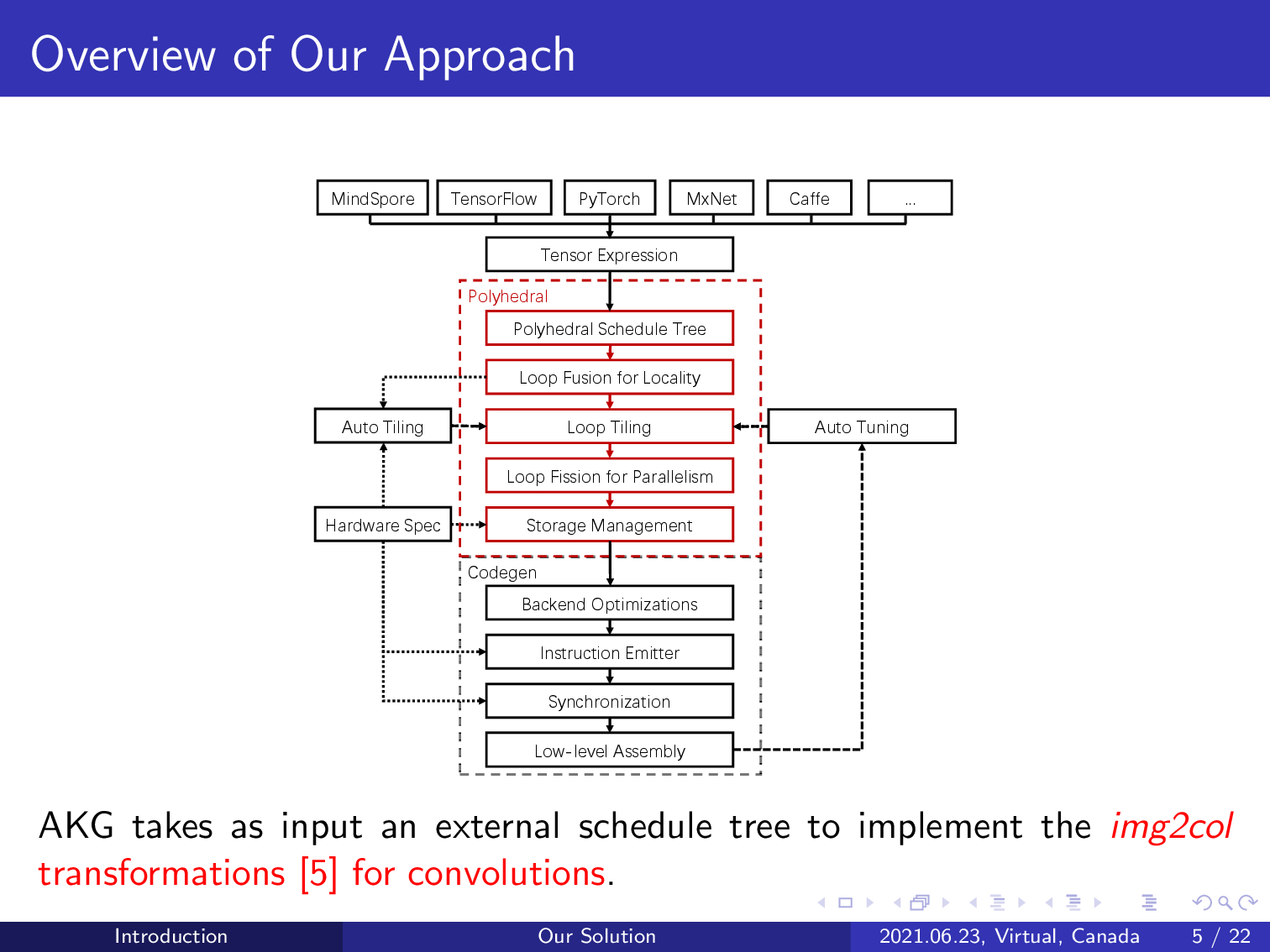
AKG implements domain-specific transformations including image to column and fractal unrolling to improve the performance of convolution operations.
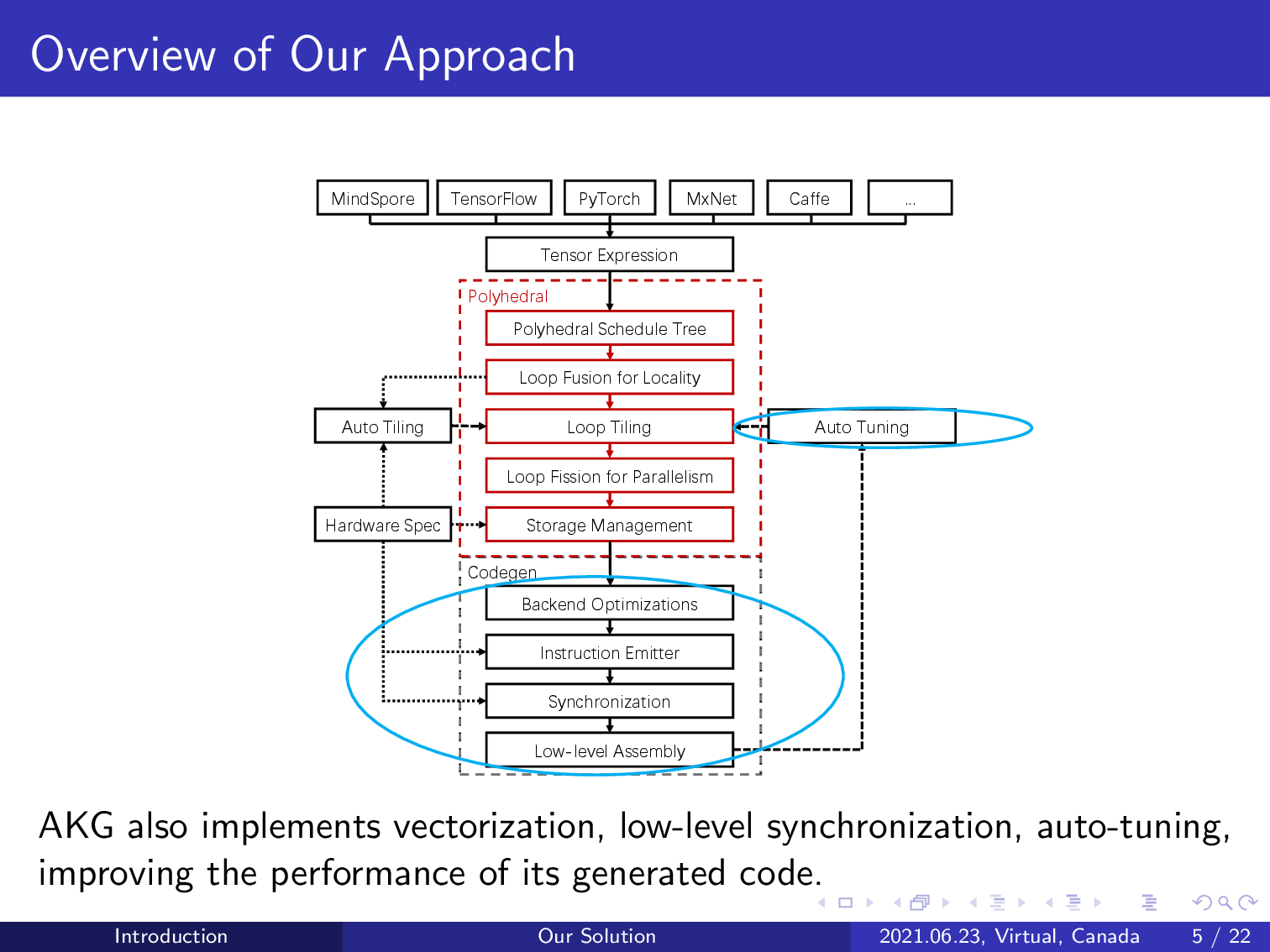
Finally, we complement the power of AKG by implementing post-polyhedral transformations like automatic vectorization, low-level synchronization, and auto-tuning, further improving the performance of the generated code.

Before diving into the details of our compiler, I’d like to first introduce the polyhedral model. The polyhedral model is a mathematical abstraction used to analyze and optimize programs. It is well-known for its power to compose different loop transformations.

We make a tensor program written by the DSL of TVM amenable to the polyhedral model by lowering it to a polyhedral representation schedule tree, which expresses the semantics of a tensor program using a tree structure. We use this tensor program as an illustrative example. This configuration is a typical fused pattern obtained from the graph engine of TVM.

Recall that our compiler reuses the graph engine of TVM, which splits a computation graph obtained by a deep learning framework into multiple subgraphs, and our compiler works by taking each of such subgraphs as input. To make the code more clear, we show the pseudo code here where the statement IDs have also been marked. This program performs a 2D convolution followed by two vector operations on the input feature map. A constant addition is also used before the convolution.

The schedule tree is built using the textual order of the fused subgraph.
A schedule tree representation is composed of various node types. The root domain node is used to collect the full set of statement instances of the program, and it is separated by each filter node which serves as the root of a subtree. A band node is used to dictate the execution order of its parent domain or filter node using affine relations, and a sequence of set nodes is used to express the given or arbitrary order of its parent. Besides, the schedule tree also provides extension nodes and mark nodes which we will use to implement complex tiling techniques and a novel composition of loop tiling and fusion. An extension node is used to introduce statements that are originally not scheduled by a tree or subtree, and the mark node can be used to attach and cancel information which is reliably used to aid the code generation’s precision.

As we introduced earlier, AKG initially uses the versatile schedulers of the polyhedral model to exploit parallelism and locality simultaneously. Given such an initial schedule tree, AKG uses the integer linear programming-based scheduler of the ISL library to compute a new schedule for the program, and the resultant schedule tree looks like this. ISL is an integer set library that many polyhedral compilers use to perform scheduling and loop transformations. AKG also uses it as a fundamental tool.

For reference, we also display the code corresponding to the transformed schedule tree. We use the polyhedral model because it exposes a broader set of affine transformations than manual schedule templates.

For instance, loop skewing, shifting, and scaling are not expressible in TVM. Also note that all statements except S0 are fused into one group in the transformed code, and this basic fusion is performed by the library.
Now, let’s delve deeper into the transformed schedule tree suggested by the ISL scheduler.
It suggests two fusion groups, so the code generator will produce two kernels by scanning this schedule tree.

According to our previous study, all of the statements can be fused into a single fusion group. In other words, one would receive more memory transfer time if the code generator can produce a single group. We divide the fusion group into two categories: integer intermediate and level. A leaf out iteration space contains at least one statement to write values to variables that will be used outside the program, and all values defined by the statement of an intermediate iteration space will be consumed by the program.

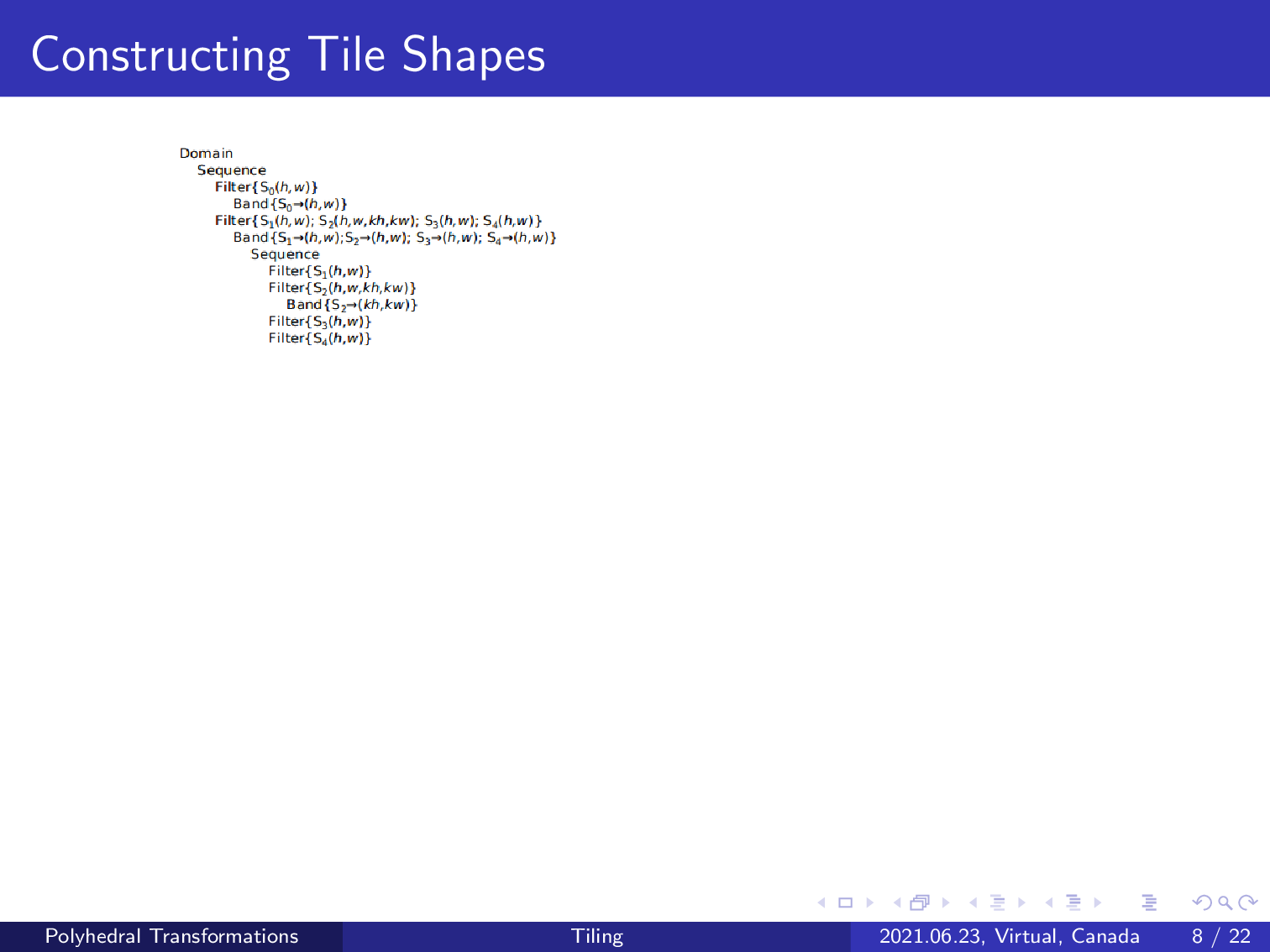
According to the tradition of polyhedral compilers, one should perform loop tiling to each iteration space. We did not follow this workflow but only tiled the level iteration spaces as shown in the red part. This performs classical rectangular tiling to the level iteration space, and one can compute the memory footprint required by each tile, which can be expressed using this affine relation.
The content you provided is already in English. Therefore, according to your instructions, I will output it as-is without translation:

As tensor A is written by the statement S0, one can concatenate this affine relation with the read access relation between statement S0 and tensor A, which will give us the relation between each tile of the level iteration space and the statement S0. This affine relation implies a complex tile shape.

In addition to the construction of complex tile shapes. We also present a language to allow for the manual specification of tile sizes. This is different from traditional compilers that use default sizes embedded in a compiler, or only allow tile size selection along with the manual specification of schedule templates in TVM.
The tile size specified by this language will be passed to AKG and will be automatically optimized internally, which takes into consideration the transformations modeled in the compiler.

Recall that we have obtained such an affine relation by first applying rectangular tiling on the level iteration space. The schedule tree currently has not yet applied loop tiling to the intermediate iteration space. One may find that this affine relation implies an overlapping tile shape of the intermediate iteration space, but it has to be used together with loop fusion.

As we mentioned before, we leverage the extension node to introduce this relation in the second subtree of the root domain node, as shown in the right part. This extension node performs a post-tiling fusion between the two fusion groups.
This strategy enables a novel composition of Italian fusion that was impossible in traditional polyhedral compilers.

As the final step, we introduce a mark node to the original subtree that has been fused into the second fusion group. The string of the mark node indicates that the marked subtree should be skipped when generating code. The code generated by scanning this schedule tree guarantees correctness.

Now we have a schedule tree like this and this schedule tree is sufficient for traditional memory hierarchy pyramid. However, this schedule tree cannot exploit the divergent compute units of modern AI accelerators, which require the management of the multi-directional memory hierarchy.

For your reference, we put the architecture of the NPU chips with it. One may notice that the cube vector and the scalar units require multi-directional on-chip data flow management. And again, we use the mark node of schedule trees as a hint for the code generator. All future nodes that have been marked will be processed by the vector or scalar unit, as shown in the red part.
When marking such filter nodes, we evaluate whether the enclosing statement involves a dot product. We consider statements performing a dot product as a convolution or a matrix multiplication, and these statements are passed to the cube unit while other statements or filters will be flowed to the vector or scalar unit.

One may notice that the subtree within the blue part has been distributed when compared to the schedule tree on the left.
This precisely models the inter-tile scheduling as the reverse transformation of a max fusion, which can be triggered by passing an appropriate option.

While still considering the target memory hierarchy, we have automated the complex data flow between the memory system and vector and scalar units have been fully exploited. As an operator involving a dot product will be delivered to the cube unit, we have to consider the effectiveness of our approach.
The power of the cube unit can be fully exploited when executing matrix multiplication, but the convolution operator will also be handled by this compute unit.
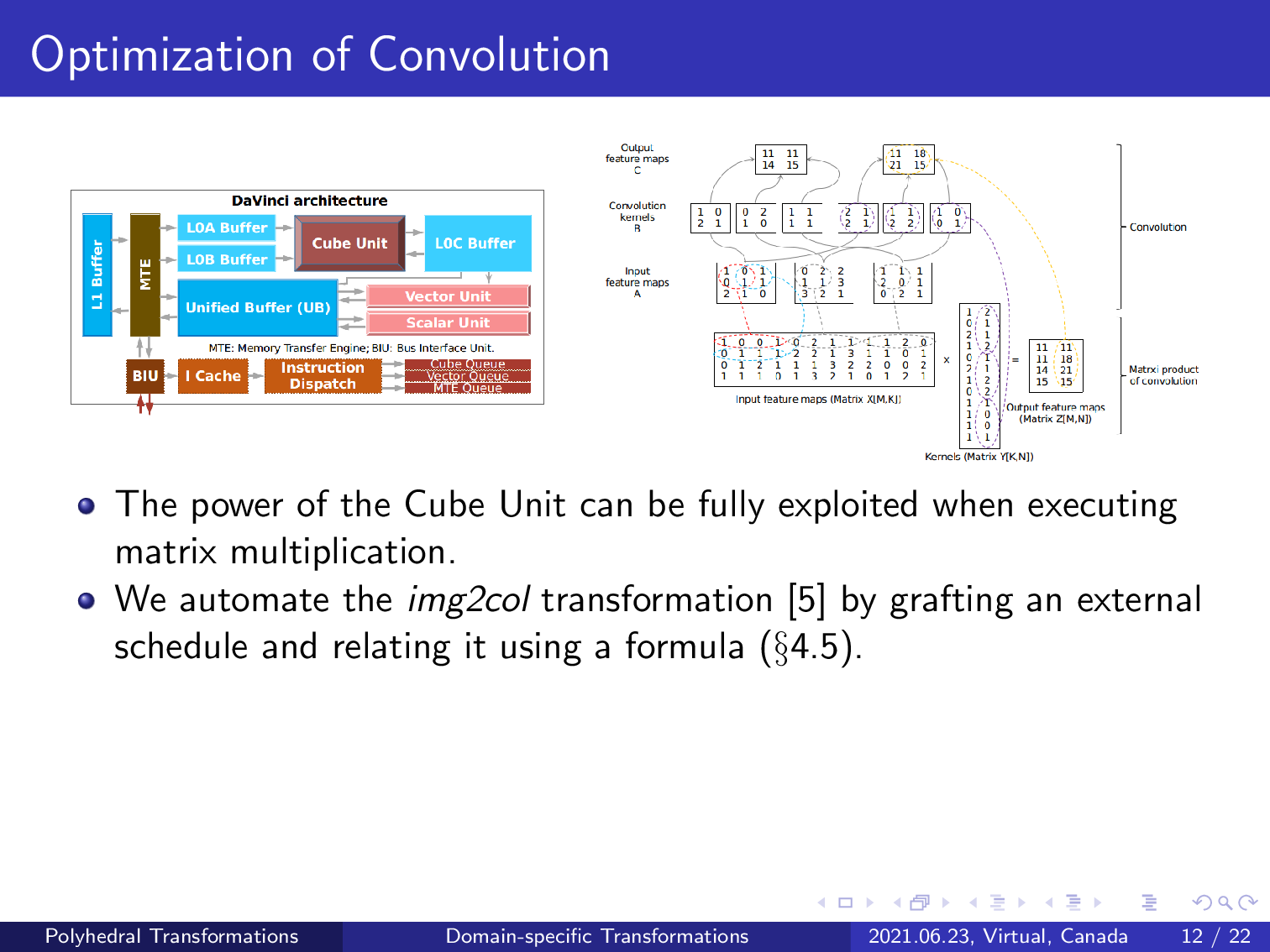
We last use the image to column transformation to convert a convolution into matrix multiplication; however, such a domain-specific transformation may alter the syntax of the counterpart in a schedule tree representation, which is outside the scope of the traditional polyhedral compilation approaches.
We automate this transformation by creating an external schedule tree that represents matrix multiplication and relates the convolution with this matrix multiplication using a predefined formula. The external schedule tree of the matrix multiplication is used to replace the counterpart of the convolution in the original schedule tree.
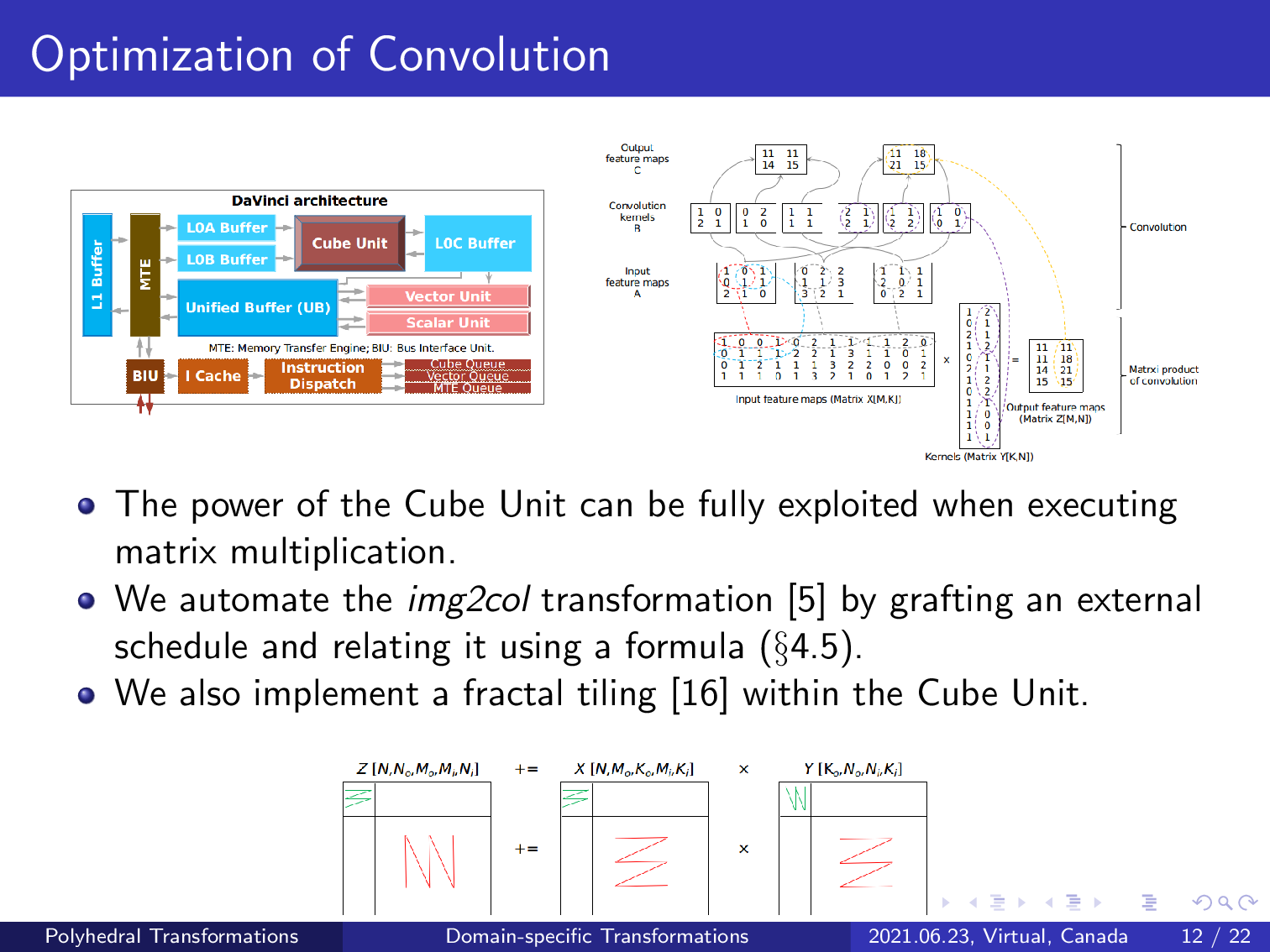
Once a convolution has been transformed into matrix multiplication, we apply fractal tiling to make it fit the cube unit and its corresponding buffer on the chip, such that the power of the compute unit and its second-level memory buffers can be fully exploited.
The figure at the bottom of the slide shows the tiling strategy used to decompose a larger matrix multiplication. The red broken lines express the execution order between tiles, and the green broken lines are used to denote the execution order in a tile.

In addition to the polyhedral transformations in the previous slides, AKG also performs other transformations at either preprocessing steps and the post-polyhedral transformations.
The preprocessing transformations include function inlining, common sub-expression eliminations, and so on.
The automatic storage management is implemented by manipulating schedule trees, and we provide a memory hierarchy specification language for manual scheduling and debugging.
Finally, we automate vectorization code generation, a dynamic programming-based synchronization between emitted instructions, and provide an auto-tuning strategy.

At the end of the talk, we report the experimental results and here is the experimental setup.
We conduct experiments on benchmarks ranging from single operators to end-to-end workflows on high-performance NPU Huawei Ascend 910 chips. Performance is compared against manually optimized C/C++ code written by experts, and the adapted TVM schedule templates developed by the software research and development team of the chip.
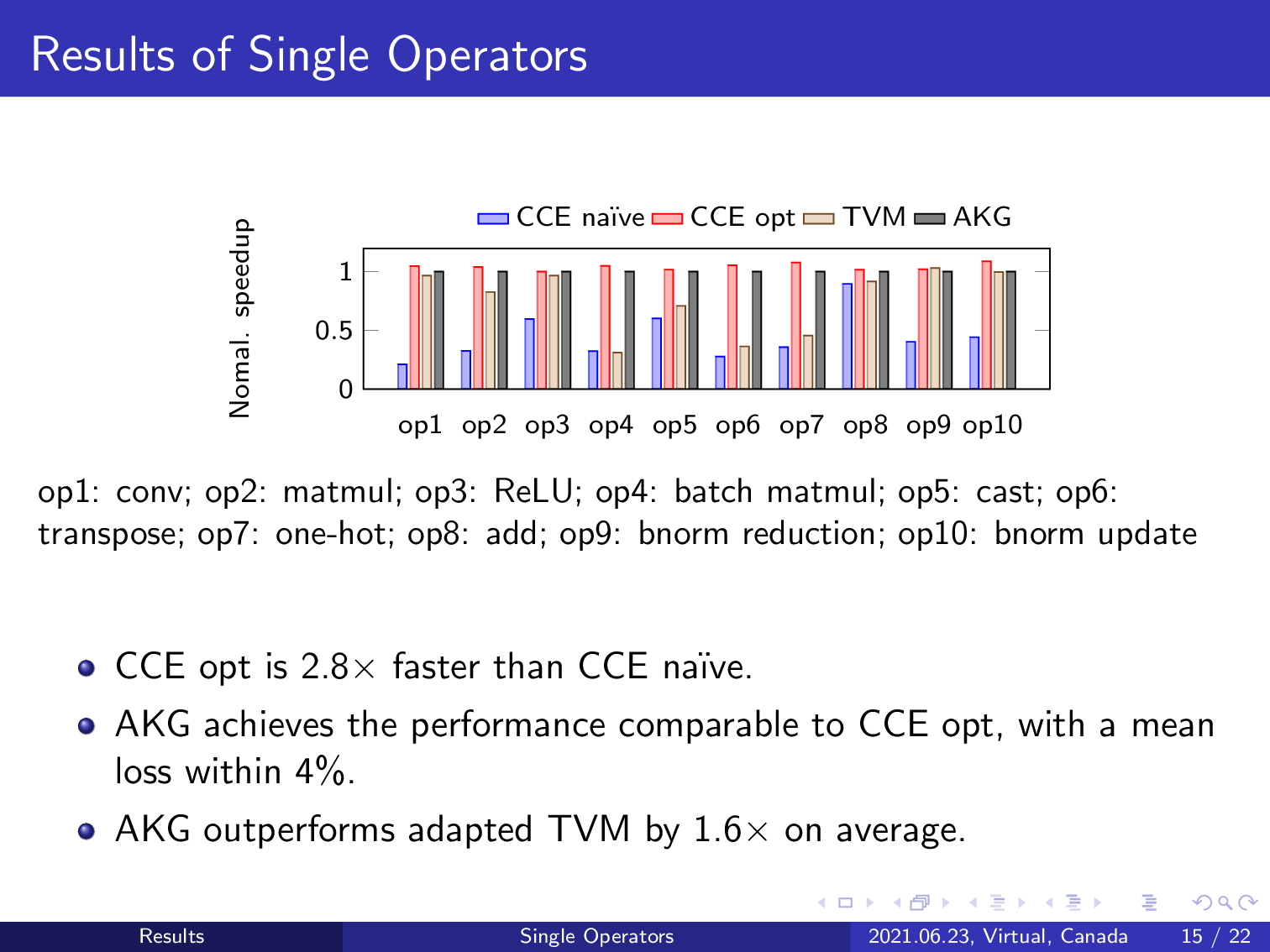
We first report the results of single operators. For the 10 single operators used in the experiment, AKG achieves comparable performance to the manually optimized code, that is 2.8 times faster than the naïve implementation. Our work obtains 1.6 times speed up over TVM on these single operators.
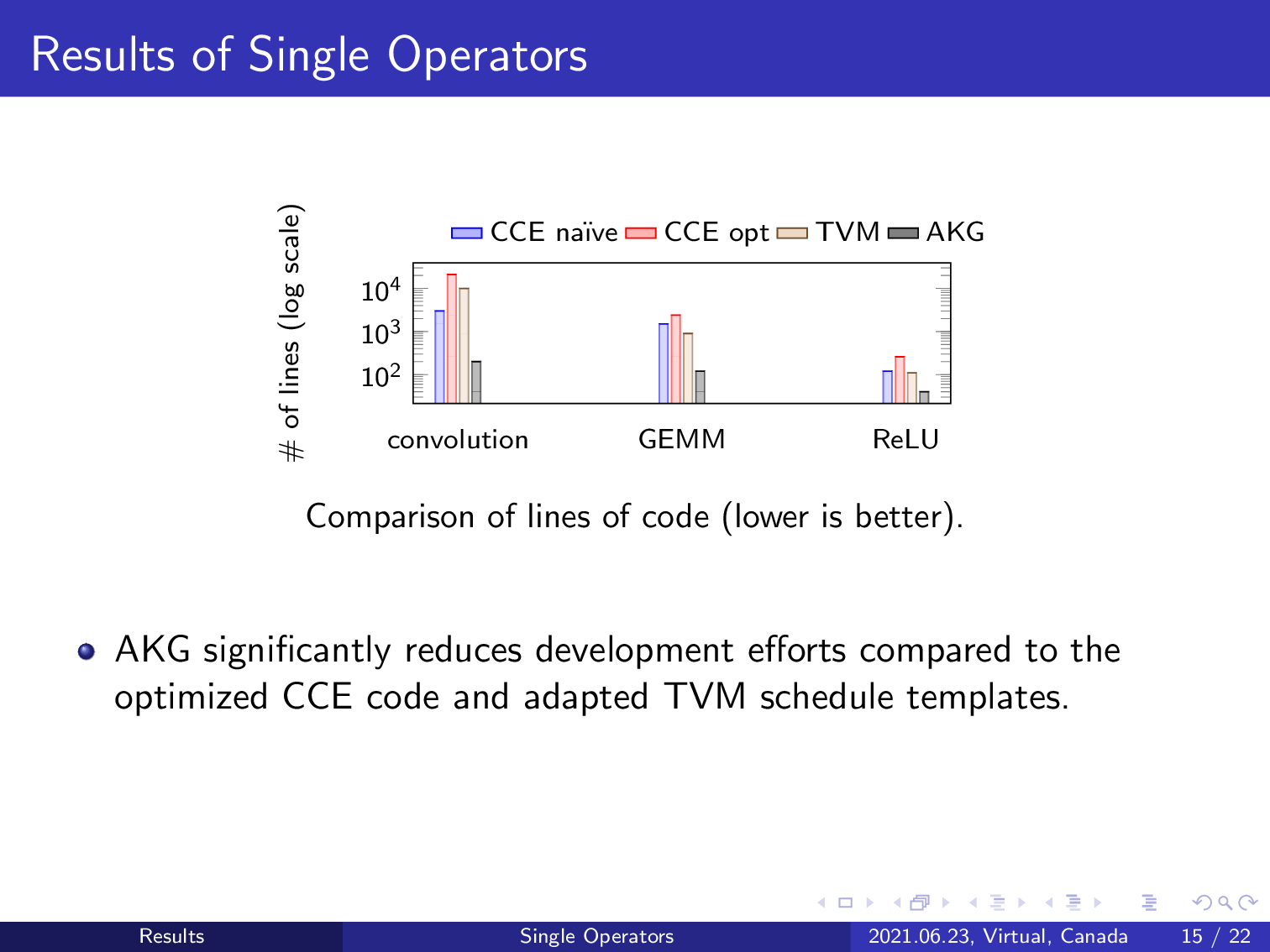
This is the comparison of lines of code. We use three typical single operators in deep learning models to illustrate the effect, which demonstrates that AKG can significantly reduce development efforts compared to optimized C/C++ code and the adapted TVM.
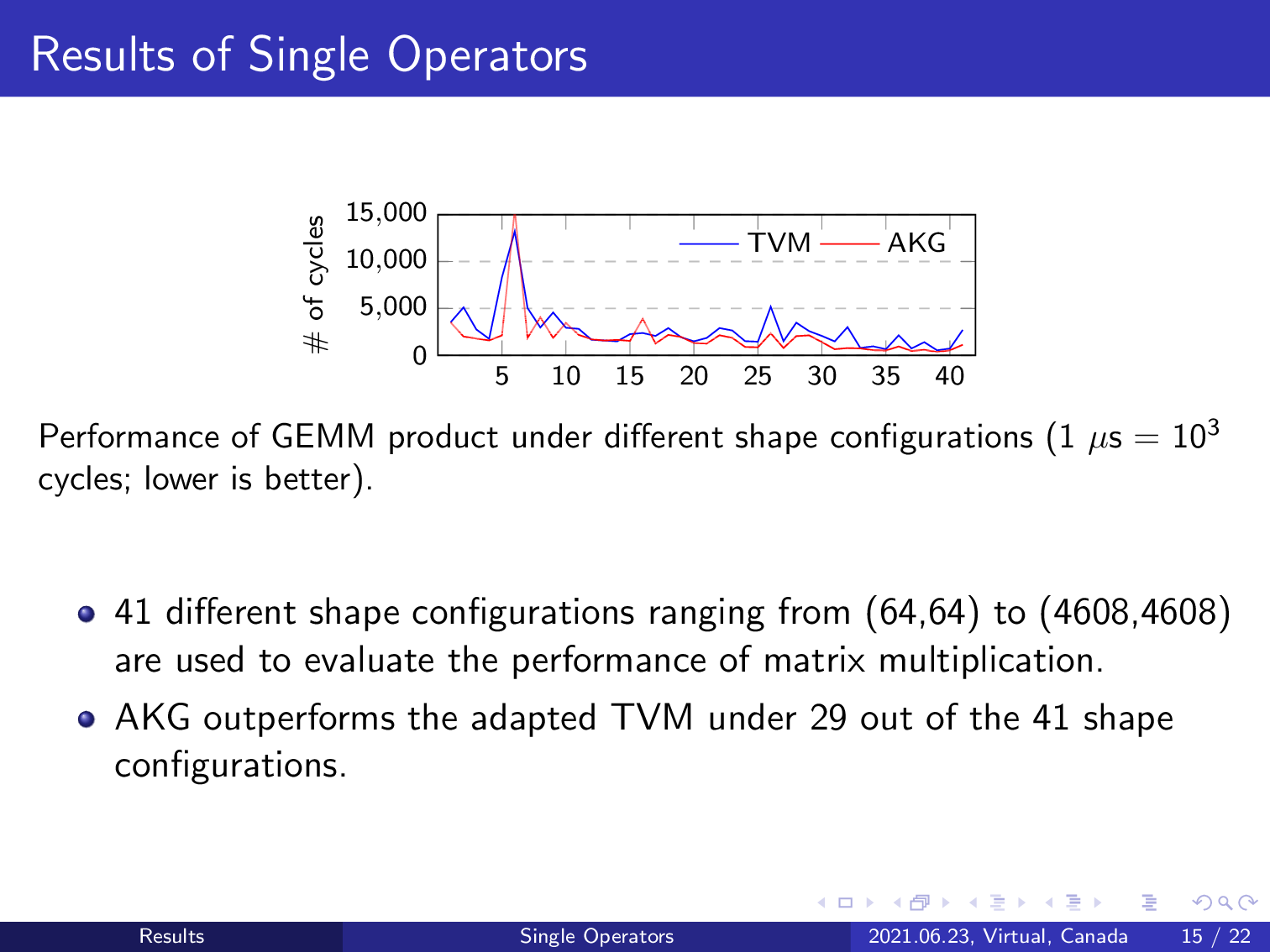
We also evaluate the effect of AKG by experimenting with matrix multiplication in 41 different shape configurations. We use matrix multiplication because it is one of the most important kernels of many applications, and more importantly, the convolution operator will also be converted into matrix multiplication by AKG. In summary, AKG outperforms TVM in 29 out of the 41 shape configurations, demonstrating the effectiveness of our approach.
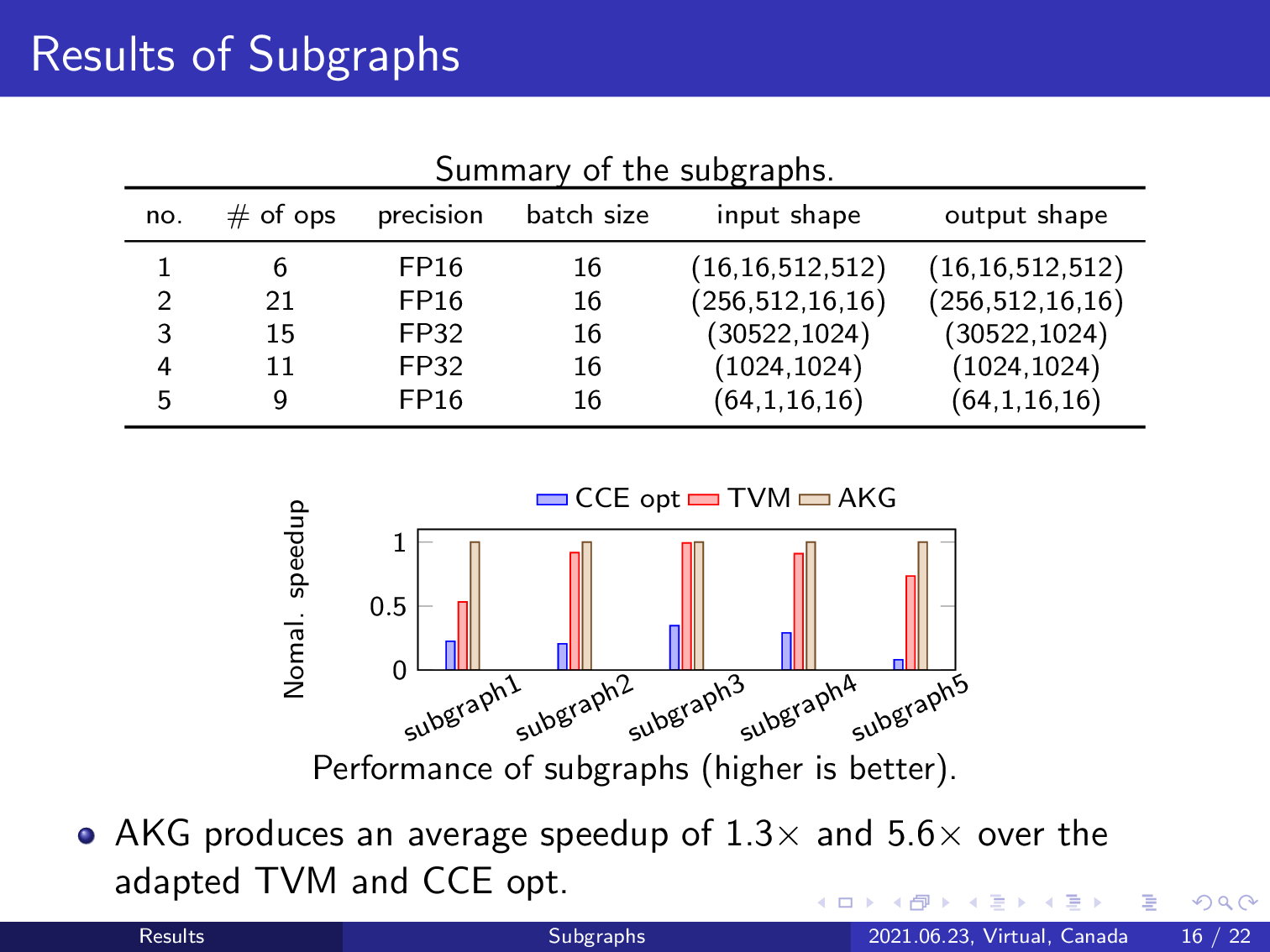
Next, we evaluate the fusion effect of AKG by conducting experiments on subgraphs generated by the graph engine of TVM. The summary of the subgraphs is listed in a table and this is the normalized speedup of different approaches. The naïve version is excluded because the developers of the NPU chips did not provide the code. AKG achieves an average speedup of 1.3 times and 5.6 times over TVM and the manually optimized implementation, respectively.
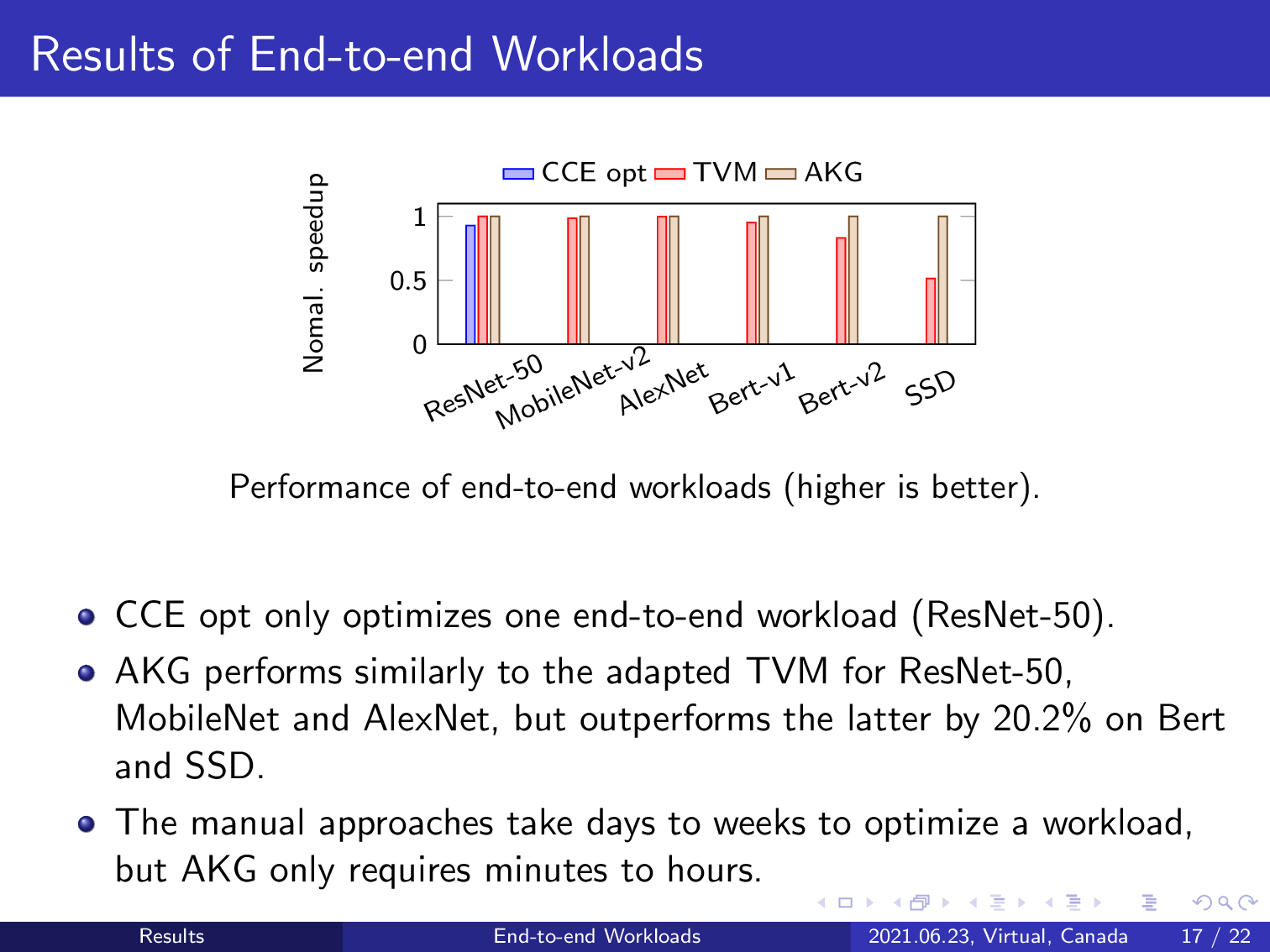
And for end-to-end workflows, AKG performs similarly to TVM for ResNet-50, MobileNet, and InceptionNet, and outperforms TVM by a mean improvement of 20.2% when experimented on BERT and SSD only. Contrarily, the C/C++ code only optimized one deep learning model, ResNet-50, but our approach still obtains a 7.6% improvement over it.
AKG also reduced the software development lifecycle from months to hours.
The content you provided is already in English, so according to your instructions, it should be output as-is without translation. Here it is:

We finally conclude our work using this page. The contributions of our work include a careful handling of the interplay between tiling and a hierarchical fusion approach that can be adapted to many other NPU architectures. And an automatic implementation of the domain-specific transformations for convolutions and the extension of schedule tree transformations. Schedule tree expressiveness. While the fractional tiling is domain-specific, the image-to-column transformation and the reverse strategy for post-tiling fusion and heuristics are general methods.

The full paper and the code can be obtained by scanning the following QR codes. Thank you for your interest in our work.


