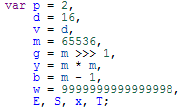Deciphering the RSA Encryption of Renren Network Login Password

There are two types of passwords in the world: one is to prevent your little sister from peeking at your files; the other is to prevent the authorities from reading your files.

—— Bruce Schneier “Applied Cryptography”
The legendary “plaintext password” comes in two forms: plaintext transmission and plaintext storage. A password transmitted in plaintext does not necessarily mean it is stored in plaintext, and a password stored in plaintext does not necessarily mean it is transmitted in plaintext. The plaintext password incident that caused a stir last year was a case of passwords being stored in plaintext. Once the website’s database was stolen, the users’ passwords were also stolen. Transmitting passwords in plaintext is also very dangerous, as many places on the network may have sniffing devices installed. To these sniffers, passwords transmitted in plaintext are no secret at all. This article focuses on the security issues in password transmission.

What is “plaintext”? If a password is sent out directly in ASCII characters, it is plaintext to anyone; if a password is encoded with base64 (for example, 123456 encoded with base64 is MTIzNDU2), it may be ciphertext to most people, but it is plaintext to any professional programmer. Some people think that if the “encryption” algorithm is made more complex and the code is obfuscated, no one will be able to analyze it. This approach is called hiding, not security, and is at the level of preventing little sisters from peeking at files. Real security depends on public, widely used cryptographic algorithms, and relies on keys rather than the algorithm itself to ensure security.

Unfortunately, cryptographic algorithms and protocols are not necessarily secure just because they are cobbled together.

Observing Renren Network Password Transmission

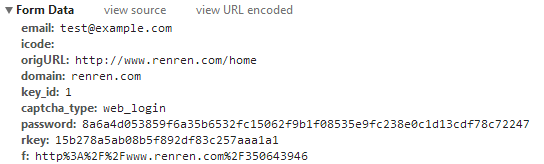
A long, long time ago, the password of Renren Network was transmitted in plaintext without any encoding. Now, the login password of Renren Network is encrypted for transmission. If you look at that HTTP POST request (/ajaxLogin/login) for logging into Renren Network in the browser’s developer tools, you will find that the password has turned into a long string.

Capture

The first thing I thought of was hash. Could it be that some operation is performed on the user’s input password and rkey, and then the hash value is taken as the password? I tried string concatenation and common hash algorithms, but it wasn’t like that. Where does this rkey come from? The /getEncryptionKey HTTP request will return some data including rkey. When I saw e: “10001”, I guessed that this might be RSA encryption, but let’s not talk about it for now.

Capture

By the way, I found a replay attack vulnerability here. After successful login, the rkey does not become invalid. Using the same POST request, you can still log in successfully on a machine on the other side of the ocean, and even if the original user logs out, it does not affect the usability of the POST login. Only by changing the password or waiting for a long enough time can this sniffed POST request become invalid. For script kiddies who want to peek at other people’s privacy, this might be enough. But our goal is to recover plaintext passwords, so how can we stop here?

Analyzing Obfuscated JS Code

It seems that we have to look at the source code. Renren Network login is handled by login-v6.js. This JavaScript code has been obfuscated, but it looks much better after being processed by JSBeautifier. (The processed code snippet is shown in the figure below)

Capture

When I first learned programming, my teacher told us “programs should be read from the main function”, but for any program of a certain scale, if you start reading from the main function, you might have turned gray by the time you find the code snippet you care about, and it’s more likely that your brain’s stack will overflow before you find the code snippet you care about. If you don’t believe me, you can read the following code snippet (part of the RSA encryption library), and raise your hand if you understand it.

Capture

A powerful weapon for analyzing large programs might be string search (grep). These strings or magic numbers can let us know the function of this code snippet; or they are the identification strings of a certain library.

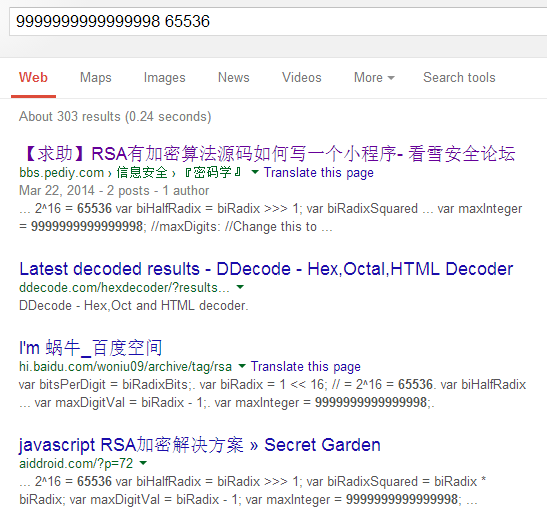
Starting from the first code snippet posted above (where the user inputs the password), you can find the second code snippet posted above, which looks like some mathematical operations. One set of magic numbers reveals the secret:

Capture

Searching these two magic numbers in Google, it is estimated to be part of a library:

Capture

Further search reveals that this is an open source RSA library implemented purely in JavaScript, and its homepage is http://www.ohdave.com/rsa/. Comparing it with the obfuscated Renren Network code, there is no doubt. The general process is as follows:

1. The browser initiates a getEncryptionKey request, the server generates a pair of 256-bit RSA public and private keys, randomly generates an rkey, and stores the public and private keys indexed by rkey.
2. The server sends back e (fixed at hexadecimal 10001), n (hexadecimal representation of the 256-bit public key), and rkey to the browser.
3. When the user enters the password and clicks login, the browser encrypts the password with the public key n and exponent e to get the password (hexadecimal representation of the 256 bits), and sends it to the server along with rkey.
4. The server retrieves the private key based on rkey, decrypts the password to get the plaintext password, and then proceeds with the regular password check process.
   Seeing the word “RSA”, many people may think that cracking is hopeless; but when I analyzed it to this point, it seemed as if I saw the dawn of victory.

Why RSA needs long keys

In 1976, Diffie and Hellman published the world’s first public secret generation protocol based on public keys, opening a new page in the history of cryptography. Before this, people always believed that it was impossible to achieve secure communication on a monitored channel without a common secret in advance, and the Diffie-Hellman protocol is an algorithm to securely generate a common secret on a monitored channel. A year later, in 1977, Rivest, Shamir, and Adleman published the RSA public key encryption algorithm.

Public key cryptography is essentially based on some long-standing mathematical problems, such as the knapsack problem, the discrete logarithm problem, and the factor decomposition problem. The Diffie-Hellman algorithm is based on the discrete logarithm problem, while the RSA algorithm is based on the factor decomposition problem. Each public key is a mathematical problem. As long as the attacker manages to solve this problem, they can get the private key and decrypt the information. This is completely different from what we usually call “encrypting with a password” (scientifically symmetric encryption).

The security of symmetric encryption depends on the confidentiality of the password. For the ideal symmetric encryption algorithm, all passwords can only be decrypted by exhaustive search, so a random password of 16 uppercase and lowercase letters plus numbers is roughly equivalent to 96 bits binary, which means that on average, it would take four trillion trillion trillion trials to guess the password, which is impossible in a lifetime. And a 96-bit (binary) scale mathematical problem is not a problem at all in front of a computer, and it is enough to decompose such a large composite number in 1 second.

We often see RSA keys as long as 2048 bits, 4096 bits, while symmetric keys of 128 bits, 256 bits are enough, public keys are often much longer than symmetric keys, this is the reason.

Let’s take a closer look at how RSA works. First, find two large prime numbers p and q of the same number of digits, calculate their product pq as the public key n. Calculate φ(n) = φ(p)φ(q) = (p − 1)(q − 1). Choose e that is coprime with φ(n) as the exponent. The information (message) to be encrypted is set as m, m^e mod n is the ciphertext. For fast encryption, this e is generally a fixed value, such as e = hex 10001 = 65537, so encryption only requires 17 multiplications.

When decrypting, find d such that de mod φ(n) = 1, this can be quickly obtained by the Euclidean algorithm, no more to say. Just calculate the d-th power of the ciphertext c^d mod n to restore the plaintext m. Here d is the private key. The mathematical principle here is m^{ed - 1} mod n = 1, which is due to the property of the Euler function φ(n), those interested can refer to Wikipedia.

We already know that the RSA public key n is the product of two large prime numbers p and q. As long as these two prime factors are found, the private key d can be obtained, and then the information can be decrypted. Renren.com uses a 256-bit RSA public key, which is a 77-digit decimal integer, which can be decomposed in two or three minutes on a personal PC. This is the terrifying aspect of short public keys.

Factorization of Prime Factors

The method of factorizing prime factors that we have all learned is trial division, trying one by one from 1 to the square root of n. For a 77-digit decimal integer, it needs to be tried 10³⁸ times, which is obviously unacceptable.

Fermat’s Difference of Squares

Fermat’s prime factorization algorithm is the first major improvement after trial division and sieve methods. The starting point of this algorithm is the difference of squares formula (a-b)(a+b) = a² - b². If we can find two positive integers u and v less than n, u + v ≠ n, and (u² - v²) can be divided by n, then (u+v)(u-v) can be divided by n. Since n is the product of two prime numbers p and q, and neither u+v nor u-v can be divided by n, then the two factors p and q have to be divided between u+v and u-v. The greatest common divisor of u-v and n is either p or q. Calculating the greatest common divisor of u-v and n is a fast process, with a time complexity equivalent to multiplying them.

For example, n = 2041, u = 1416, v = 311, it can be verified that (u² - v²) can be divided by n, then take the greatest common divisor of u-v and n (1416-311, 2041) = 13, 13 must be a prime factor of n. In fact, 2041 = 13 × 157.

The question is, where to find such u and v? One method is to let u = sqrt(n) (round up the square root of n, i.e., u is the smallest positive integer not less than the square root of n), and see if (u² - n) is a perfect square. If it is, then u² - n = v². If not, incrementally test larger n. For example, n = 2041, sqrt(n) = 46, the test process is as follows:

• 46*46 - 2041 = 75
• 47*47 - 2041 = 168
• 48*48 - 2041 = 263
• 49*49 - 2041 = 360
• 50*50 - 2041 = 459
• 51*51 - 2041 = 560
• ……
  Obviously, this path won’t go far.

It’s also okay if the product is a perfect square

In the above (u² - n), if the product of some of them is a perfect square, then it’s okay. In the above example, suppose we suddenly find that 75 * 168 * 360 * 560 is a perfect square, then (46² - 2041) * (47² - 2041) * (49² - 2041) * (51² - 2041) = 75 * 168 * 360 * 560 = 50400².

Notice that the square relationship we want to find is mod n, so we have 46² * 47² * 49² * 51² mod 2041 = 50400² mod 2041, which is (46474951)² mod 2041 = 50400² mod 2041. u = 46474951 mod 2041 = 311, v = 50400 mod 2041 = 1416, these are the u and v we are looking for.

The question comes again: how to find out which product of 75, 168, 263, 360, 459, 560… is a perfect square? The clever reader may think of factoring these numbers into prime factors, and then just find several numbers so that the sum of the powers of each prime number in their prime factor decomposition is even, the product of these numbers is a perfect square. For example

• 75 = 3 * 5²
• 168 = 2³ * 3 * 7
• 360 = 2³ * 3² * 5
• 560 = 2⁴ * 5 * 7
  The sum of the powers of the prime factors 2, 3, 5, 7 in the above four numbers are 10, 4, 4, 2, all even, so their product = (2⁵ * 3² * 5² * 7¹)² is a perfect square.

Sieve out “easy to decompose” numbers

Factoring prime numbers is not easy, even for (u² - n) which is quite close to n, it is still quite time-consuming. But we are already close to the end! We can only consider numbers that can be divided by relatively small prime numbers. If we want to find numbers in the range of 1N that can be divided by primes less than B, the most commonly used method is the sieve method, which we have used when finding primes in 1N. First cross out all multiples of 2, then all multiples of 3… After crossing out all multiples of primes, the remaining ones are all primes.

Now what we want are the primes in the sequence of (u² - n) formed by u=0,1,2… The sieve method can still be used after a slight modification. When crossing out multiples of p, we don’t need to try dividing by p one by one. If (u² - n) can be divided by p, then u² mod p = n mod p. Since p is a prime number, there are at most two u less than p (of course, there may be none). After finding a u with a relatively fast algorithm, (n - u)² mod p = n mod p, we find another u, which can be called -u in the sense of mod p. Based on ±u plus multiples of p, its square mod p is still congruent to n. Therefore, we only need to cross out the elements with array indices u, u+p, u+2p, u+3p… and -u+p, -u+2p, -u+3p… to sieve out all multiples of p.

Since we are doing prime factor decomposition, we can’t delete these multiples of p, but need to keep dividing by p until it can’t be divided anymore, so we get the power of p in this element.

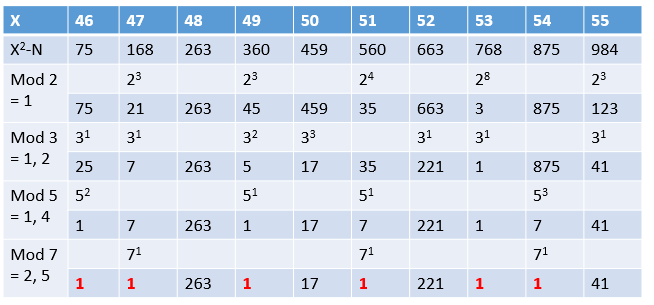
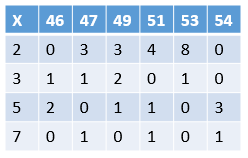
For example, for n = 2041, take B = 10, that is, only find primes less than 10, namely 2, 3, 5, 7. If a (X² - n) becomes 1 after passing through the sieve, it means that this number can be completely decomposed into the product of 2, 3, 5, 7; otherwise, this number is not considered.

Capture

Take out the numbers in the above table that can be completely decomposed, and record their powers of 2, 3, 5, 7:

Capture1

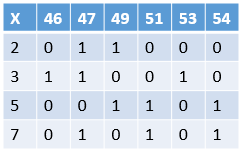
Finding the Product of Squares

Since our goal is to find a product of several numbers that is a square, that is, the sum of the powers is even, we are only interested in the parity of the powers, so we mod 2 to get the following table:

Capture2

We need to find several columns so that the sum of these columns is even, or the sum of these columns mod 2 is a zero vector. Isn’t this a standard system of linear equations? Yes, the Gaussian elimination method can come in handy (in fact, the more efficient Lanczos algorithm can be used).

We get three non-trivial solutions: (46, 47, 49, 51), (51, 54), (46, 53), in fact, one solution is enough. These three solutions each correspond to a pair of (u, v), and then get the prime factors of n = 2041:

• (46, 47, 49, 51): 464749*51 mod 2041 = 311，2³ * 3² * 5² * 7 mod 2041 = 1416，(1416 - 311, 2041) = 13
• (51, 54): 51*54 mod 2041 = 713，2² * 5² * 7 mod 2041 = 700，(713 - 700, 2041) = 13
• (46, 53): 46*53 mod 2041 = 397，2⁴ * 3 * 5 mod 2041 = 240，(397 - 240, 2041) = 157
  In actual calculations, decompositions like 459 = 3³ * 17 may not necessarily be discarded. The remaining 17 can be stored in a temporary table. If there is another number that also decomposes 17, such as u = 52 when 663 = 3 * 13 * 17 (assuming the set of primes used for sieving includes 2, 3, 5, 7, 11, 13), this 17 has a pair and is still usable. If no pair can be found, the number that cannot be completely decomposed can only be discarded.

The above algorithm is basically based on elementary number theory and is not complicated, but this algorithm, known as the quadratic sieve, is still the fastest algorithm for prime factor decomposition of decimal numbers less than 100 digits.

Real-world RSA Decomposition

Many scientific computing software have built-in large number decomposition functions, and there is no need to implement high-precision calculations yourself. Here I used a small open-source tool msieve, which implements prime factor decomposition algorithms including the quadratic sieve.

Take the Renren public key given earlier for decomposition:

1

$ ./msieve 0x8ca2ddaf2a8da3c3c6ed795b87eca0d33827c82b31b6282a5045bc75e9b83153

On a personal PC with Core i7 (msieve is single-threaded), it took 2 minutes 55 seconds (using different 256-bit RSA keys for testing, the decomposition time is between 2 and 4 minutes), and the complete output is as follows.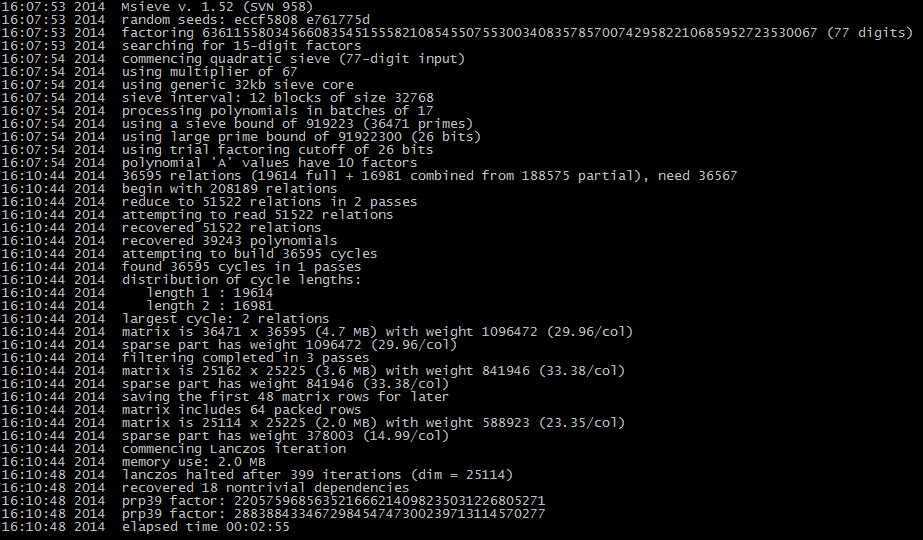
Capture

Of these, the first 170 seconds are used to sieve out “easy to decompose” numbers, and the last 4 seconds are used to solve the system of linear equations. From this output, we see that in order to decompose this 77-digit integer, B = 919223 is chosen, that is, 36471 primes below B are used for sieving. The range of u being sieved is 12 * 32768 = 393216. Among these u, 19614 numbers that can be completely decomposed within the range of B were found; there are also 188575 numbers that cannot be completely decomposed, but their “tails” after removing all primes below B can be paired, forming 16981 pairs of “tails”. After some optimization, a matrix of about 20,000 orders is obtained, and the prime factor decomposition of n is obtained: 220575968563521666214098235031226805271 and 288388433467298454747300239713114570277 (decimal), both of which are 39-digit integers.

The moment to witness the miracle is coming. First, calculate φ(n) = (p-1)(q-1), and then calculate the multiplicative inverse element d of e = 65537 under mod φ(n):

Capture

Then bring in the ciphertext (password in the HTTP POST request) c = 0x8a6a4d053859f6a35b6532fc15062f9b1f08535e9fc238e0c1d13cdf78c72247, calculate c^d mod n, and you get the plaintext password 0x64726f7773736150656854746f4e734973696854.

Capture1

Displayed in ASCII characters, it is drowssaPehTtoNsIsihT. The RSA library used by Renren Network converts the password string into an integer, where the beginning of the string is the low bit and the end of the string is the high bit. Therefore, the password we just entered is ThisIsNotThePassword. Task completed!

The vulnerability is not over yet

If the programmers of Renren Network changed the RSA key to 2048 bits and then went to sleep, then this encryption is still vulnerable. We assume that the user’s password is ruby1111 (by the way, many people are using a password of four letters plus four digits, right?), according to the method of the RSA library used by Renren Network, when the string length is not enough, zero is added at the end, which becomes a high bit after becoming an integer. That is, the message m used for encryption is 0x3131313179627572.

We factorize m = 0x3131313179627572: m = 2 * 17 * 397 * 193679 * 1355887523. These factors can be combined into two close integers: m = 2614279142 * 1355887523, both of these integers are within 2³², let a = 1355887523, b = 2614279142. Since c = m^e mod n = (a^e mod n) * (b^e mod n) mod n, we have (c / (a^e mod n)) mod n = b^e mod n. That is, as long as we find a and b within the range of 2³² that satisfy the above equation, we can restore m.

Why is such an attack effective? First, a considerable proportion of large integers can be decomposed into the product of two integers that are not much different, which makes the above “table hitting” attack possible; secondly, the above attack recovers plaintext of length L, only needs O(2^L/2) time and space complexity, that is, the effective length of the password is halved.

Do not pass plaintext directly into the RSA algorithm

Cryptographic textbooks and Wikipedia seem to take plaintext directly as m, and directly multiply e power mod n as ciphertext. In widely used encryption standards such as PKCS, either the plaintext is padded with random bytes to the number of bits of n, or another random string is generated as m, and then m is used as the symmetric key to encrypt the plaintext.

The simplest modification method for the RSA library used by Renren Network to defend against the above attacks is to imitate the original version of PKCS, not to add zeros before the plaintext password, but to first add a 0xFF byte, and then fill it with non-0xFF random bytes to the number of bits of n (such as a 2048-bit public key, padded to 256 bytes). The pseudorandom number generator here must use a better seed, and it must not be made into a deterministic sequence. After the server decrypts, find the first 0xFF from the high bit, and the original plaintext password is behind this 0xFF. Of course, there is a timing attack in the process of finding 0xFF, but it is not realistic on the Internet to use this information to recover plaintext by sending a large number of requests.

Conclusion

I don’t want this article to cause any trouble for the programmers of Renren Network. It’s a good idea to think about using public key cryptography to encrypt and transmit passwords. However, cryptography is really a professional field. Issues such as key length and message padding require understanding the mathematical principles behind the algorithm.

There are countless examples of weak encryption protocols created by large companies. We are not cryptographers, so don’t design encryption protocols by ourselves, and don’t try to “optimize” encryption algorithms cleverly. We must use time-tested cryptographic libraries, such as OpenSSL, GnuPG. Because there is no mature cryptographic library on the browser side, Renren Network uses a library that looks good in code quality, and the programmer really can’t be blamed.

Finally, here is something for everyone to show off: the time complexity of the quadratic sieve method introduced in this article is exp(sqrt(log N * log log N) / 2), where N is the number to be decomposed. It is higher than any polynomial algorithm and lower than exponential complexity. Next time someone asks “Is there an algorithm that is slower than a polynomial algorithm and faster than the best known algorithm for NP complete problems”, you can use this to show off. In fact, the time complexity of the best known algorithm for the factorization problem in the asymptotic sense (number field sieve) is also higher than any polynomial algorithm and lower than exponential. The time complexity of the factorization problem is an open question.

References

1. msieve, sourceforge project: http://sourceforge.net/projects/msieve/
2. Carl Pomerance, A Tale of Two Sieves, NOTICES OF THE AMS, December 1996: http://www.ams.org/notices/199612/pomerance.pdf
3. Carl Pomerance, Smooth numbers and the quadratic sieve, Algorithmic Number Theory, MSRI Publications, Volume 44, 2008: http://library.msri.org/books/Book44/files/03carl.pdf
4. Dan Boneh, Twenty Years of Attacks on the RSA Cryptosystem: http://crypto.stanford.edu/~dabo/pubs/papers/RSA-survey.pdf
5. Bruce Schneier, Applied Cryptography, 2nd Edition
6. Wikipedia
7. StackOverflow