How Bitcoin Works
Bitcoin, after experiencing two drastic rises and falls in April and November last year, has become more than just a toy for IT guys, but a focus of debate among all sectors of society. However, most articles about the technical principles of Bitcoin are superficial. During the New Year’s chat with good friends, we raised these questions, hoping to understand after reading this article:
- How to verify a Bitcoin transaction to make it undeniable?
- How to avoid spending a Bitcoin twice?
- If I alone have 10% of the network’s computing power, is it possible to rewrite history?
- Why do Bitcoin transactions have to wait for tens of minutes?
- How does Bitcoin ensure a limited quantity (21 million)?
- How to ensure exactly one Bitcoin is mined every 10 minutes?
- What does it mean to mine 0.1 Bitcoin at a time?
- Does a transaction of 10,000 Bitcoins require generating 10,000 transaction information?
- With such a large volume of Bitcoin transactions, how are transaction records transmitted and stored?
(If you are not familiar with Bitcoin, please refer to Wikipedia or Baidu Encyclopedia first)
Digital Signature: The Foundation of Bitcoin
For any electronic currency, the primary issue is to make transactions unforgeable and undeniable. In daily life, transactions are often realized through handwritten signatures. In the network world, we use “digital signatures”. “Applied Cryptography” [3] lists some necessary features of digital signatures:
- Trustworthy. The recipient of the signature believes that the signer has signed.
- Unforgeable. It is the signer, not someone else, who signed.
- Non-reusable. Criminals cannot move the signature to other files.
- Unchangeable. The content of the file (transaction amount) cannot be changed after signing.
- Undeniable. The signer cannot claim afterwards that he did not sign.
If Alice has a password and tells Bob, now both people have this password, it is unclear who this password belongs to. It is difficult to think of a signature method that satisfies the above 5 items without relying on a third party using traditional methods. In 1976, Diffie and Hellman’s public key cryptography [4] allowed two strangers to implement secret communication without any common secrets, making digital signatures possible.
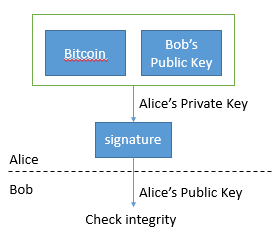
The two parties involved in the transaction each hold a pair of public and private keys, the public key is public, and the private key is held by themselves. A plaintext message can be encrypted with a private key and then decrypted with a public key (note, different from encrypted communication). Alice wants to give Bob a Bitcoin, Alice encrypts the information “this Bitcoin (a string of information) to Bob (Bob’s public key)” with her own private key, and the result is passed to Bob. What Bob gets is a Bitcoin. Bob uses Alice’s public key to decrypt, verifying the validity of this Bitcoin and the correctness of his own public key.
This method satisfies the five characteristics of digital signatures [3]:
- Trustworthy. Bob uses Alice’s public key to decrypt, confirming that it is signed by Alice.
- Unforgeable. Only Alice knows her private key, and it is impossible to derive the private key from the known public key.
- Non-reusable. The result obtained is a function of “Bitcoin + Bob’s public key”, which cannot be obtained from other Bitcoins or the public keys of people other than Bob.
- Unchangeable. If the result changes in any way, Bob will not be able to decrypt with Alice’s public key.
- Undeniable. Bob can use Alice’s public key to decrypt and verify Alice’s signature without Alice or any third party.
The fifth feature has some problems. What if Alice says afterwards that this is not my public key? In the traditional digital signature mechanism, the undeniable nature of Alice’s public key is solved by a trusted third party; but in a completely decentralized system like Bitcoin, third parties are neither allowed nor needed. In fact, Alice’s public key is in the Bitcoin. Considering the source of this Bitcoin from Alice, if we don’t consider the situation of mining by herself, then it is given by others, then Alice’s public key is already stored in the Bitcoin in the last transaction.
Bitcoin = Transaction History Chain
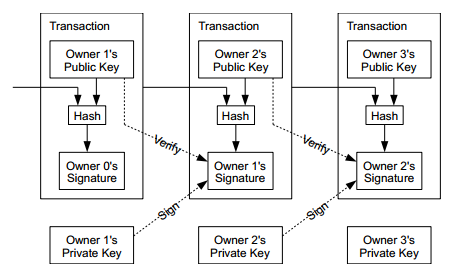
In fact, Bitcoin is a chain of digital signatures formed by the above transaction process. As long as the “original source” of Bitcoin is verifiable, the entire Bitcoin, that is, this transaction process, is verifiable.
Since digital signatures and signature verification are relatively resource-consuming, we do not want a Bitcoin to become larger and larger after a long period of circulation, and the content that needs to be signed each time becomes more and more. Therefore, what is actually signed during each transaction is the Hash value of “the original Bitcoin + the buyer’s public key”. The Hash used for cryptography is a class of one-way functions f(A) = B, knowing B is difficult to ask for A, knowing A is also difficult to find A’ so that f(A) = f(A’). This improves performance without compromising security.
Preventing Double Spending
Attentive readers may have already noticed that the above signature mechanism cannot prevent someone from spending the same Bitcoin twice. To prevent double spending, it is necessary to check all transaction histories to confirm that this Bitcoin has not been spent before this transaction. The easiest solution that comes to mind is to introduce a trusted central institution to save all transaction histories and check each new transaction. However, such a central institution violates the fully distributed design philosophy of Bitcoin. In the Bitcoin system, everyone can obtain all transaction histories and check them.
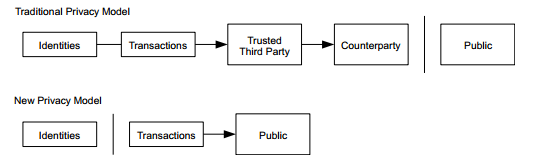
Will public transaction history destroy anonymity? No. The privacy model of Bitcoin is different from traditional financial institutions. As shown in the figure below, although all Bitcoin transactions are public, Bitcoin holders (Identities) do not contain any real-world identification information, but only a pair of public and private keys and a 34-bit Bitcoin address.
There can only be one history. Getting all Bitcoin users in the world to agree on a unique transaction history is the difficulty in designing electronic currency and the innovation of Bitcoin. Since Bitcoin is an anonymous currency, “one person, one vote” cannot be achieved by identifying real identities. One vote per IP address is nonsense, and those who have developed voting websites are deeply troubled by the constant change of IP voting machines. Bitcoin’s approach is, one CPU, one vote! Let the computer use the exhaustive method to solve the universally recognized mathematical problem, and solving a problem counts as one vote. However, now the voting capabilities of GPU, FPGA and even ASIC far exceed that of CPU, so many electronic currencies that claim to be “only CPU mining” have sprung up like mushrooms after a rain.
One CPU, One Vote
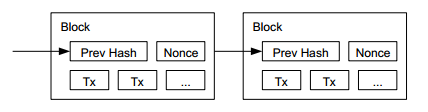
The form of the problem posed by Bitcoin is very simple: find a Nonce value so that the hash value of “Nonce value + last Hash value + transaction information to be confirmed + timestamp + target” (this is called a block, block) is less than or equal to a given threshold (called the target, target). The hash function used is SHA-256, which results in a 256-bit binary integer.
SHA-256 is a cryptographically secure hash function, which means that a slight change in the Nonce value will completely change the hash value, and a given hash value cannot be used to infer the Nonce value. Therefore, finding the Nonce value is similar to buying a lottery ticket, which is to randomly test the Nonce value. Each test will result in a basically random 256-bit binary integer. If it is less than or equal to the target, it is considered to have solved the problem. Compared with the largest 256-bit integer, the target is a very small number, for example, the target when I wrote this article is
1 | 0000000000000001A36E00000000000000000000000000000000000000000000 |
This means that on average, a new block can be found every 1.1259018e+19 attempts.
When someone announces that they have solved the problem, they must announce it widely, and other people in the world will continue to try based on the new block he generated.
Everyone’s blocks form a tree (of course, it may just be a chain). The received new blocks are always placed at the leaf nodes of the tree. The longest chain from the root of the tree to the leaf is the recognized chain. When looking for the next block, always use the hash value of the leaf node of this longest chain as the benchmark.
In the world of Bitcoin, everyone only recognizes the longest chain (block chain), that is, the transaction information contained in the longest chain is valid. The first block recognized by everyone (genesis block) is hard-coded in the Bitcoin software. Due to the longest chain rule, this block is actually no longer needed to be hard-coded, because it is already impossible to generate a chain longer than the current one from a new genesis block.
Attempts to Tamper with History
If someone tries to tamper with the transaction history of N blocks ago, they must generate a chain longer than N from the tampered block, otherwise their tampering will not be recognized. Note that this tampering cannot generate illegal transaction records (because transaction records can only be generated by holding a private key), it can only hide some legal transaction records, or tamper with their own transaction records (for example, the transaction originally given to Alice was changed to Bob), so the harm of tampering with history is limited. The following will show that as long as “the magic is high, the Tao is high”, that is, the computing power of the destroyer is significantly less than half of the total network computing power, he has almost no possibility of tampering with history.
The destroyer competes with other honest and trustworthy people in the Bitcoin network to see whose chain is longer. Each time unit, the destroyer’s computing power is p, and the probability of generating a block is p; the honest person’s computing power is q, and the probability of generating a block is q. The destroyer generates a block as +1, and the honest person generates a block as -1, then this is a classic random walk problem. When p < q, as time goes by, the probability of the destroyer winning decreases exponentially. [1] shows that when p = 1/10 * (p+q), that is, the destroyer is one-tenth of the total network computing power, the probability that the destroyer can catch up or win after the honest person has made 5 blocks is less than 0.1%; even if the destroyer’s computing power reaches 30% of the total network, the probability that the destroyer can catch up or win after the honest person has made 24 blocks is also less than 0.1%.
That is to say, as long as a transaction is written into a block, and the Bitcoin network has produced enough blocks, this history can almost never be tampered with. Therefore, a transaction only needs to wait for a sufficient amount of time to ensure its effectiveness. In practice, this time is often 60 minutes, the time required to produce 6 blocks.
Stabilizing Block Generation Speed
The target is designed to produce a new block every 10 minutes across the network. This time is short enough to allow the chain to grow at a reasonable speed and reduce the time required for transaction confirmation. It is also long enough for the person who creates a new block to broadcast it to others who are mining, allowing them to start from a new point.
The number of people participating in mining varies, and the computing power of computers is constantly improving, so a constant target is obviously not feasible. The design of Bitcoin is that the difficulty, i.e., the target (retarget), is adjusted every 2016 blocks (approximately every two weeks). If a block is generated exactly every 10 minutes, then it takes exactly two weeks to generate 2016 blocks. The Bitcoin client compares the actual time spent generating these 2016 blocks with the “two weeks” target. If the time spent is longer than two weeks, the difficulty is increased, i.e., the target is reduced; otherwise, the difficulty is reduced, i.e., the target is increased. To prevent the target from fluctuating, it is stipulated that the change in the target each time cannot exceed 4 times, i.e., the new target is not less than 25% of the original target and not more than 400% of the original target.
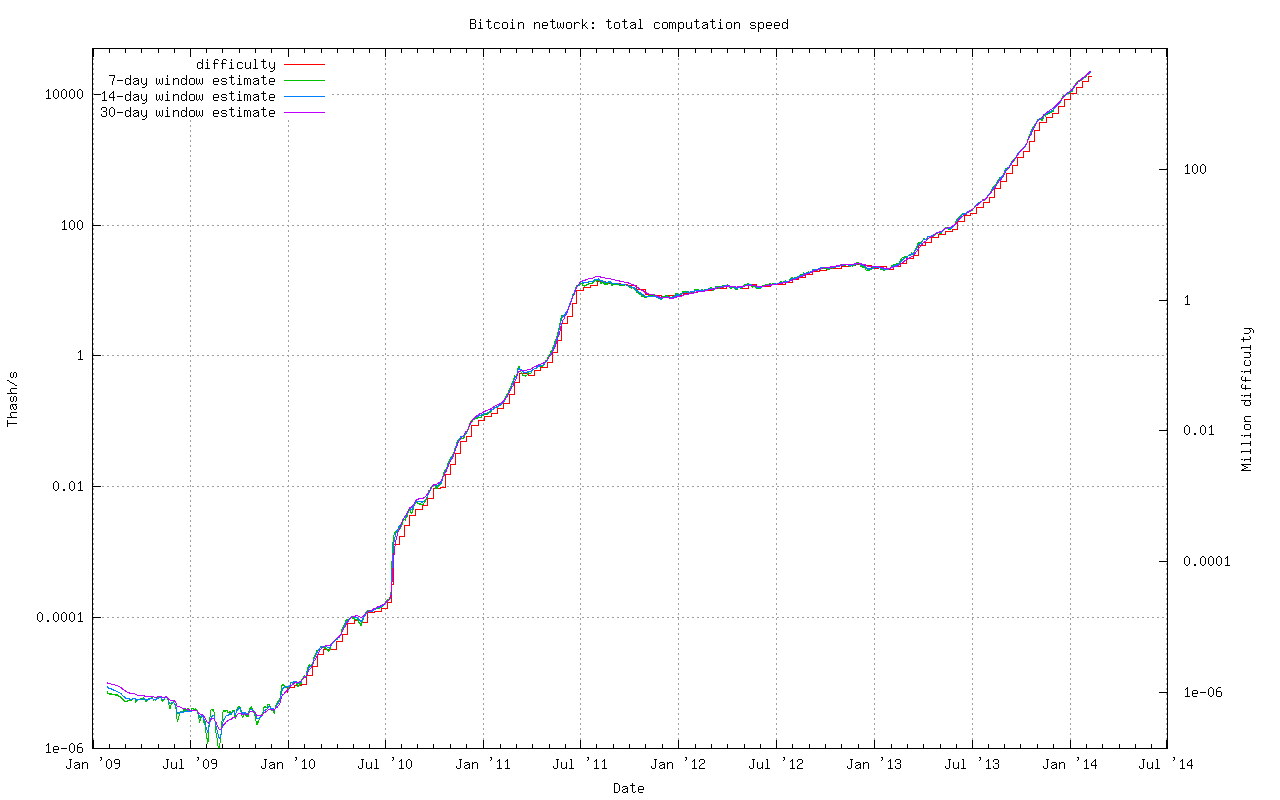
In fact, as shown in the figure below, the computing power of the Bitcoin network is mostly increasing, and the time required to generate a block is less than 10 minutes, and the difficulty is also constantly increasing. (More charts)
The target is stored in each block in the form of difficulty (difficulty = Pool Difficulty / Target), where Pool Target is a 256-bit integer, the first 32 bits are 0, and the rest are 1.
Will the adaptive change of the target give those who try to tamper with history an opportunity? If the destroyer calculates slower first, waits for the target to drop and then accelerates, will there be a greater chance of surpassing the honest person? No. Proof idea: The conclusion is obvious before the first retarget, it is impossible to prove with a quadratic function before the second retarget, and it is impossible to prove with mathematical induction and a quadratic function after the retarget.
Bitcoin Split and Merge
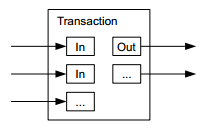
If each Bitcoin can only be consumed as a whole, and each transaction can only consume one Bitcoin, it would be too inconvenient to make large or small transactions. Therefore, Bitcoin can be split or merged during transactions. In fact, each transaction can have multiple inputs and two outputs (for simplicity, it was assumed that there was only one input and one output when explaining the digital signature chain earlier). Multiple inputs mean that multiple Bitcoins can be merged. The two outputs are the amount of Bitcoin paid to the Bitcoin buyer and the change returned to the Bitcoin seller. Obviously, the number of Bitcoins in input and output should be conserved.
Bitcoin is not infinitely divisible. The smallest unit of Bitcoin is 1/100M (one hundred millionth), named after Bitcoin’s founder, Satoshi.
Transaction History Trimming
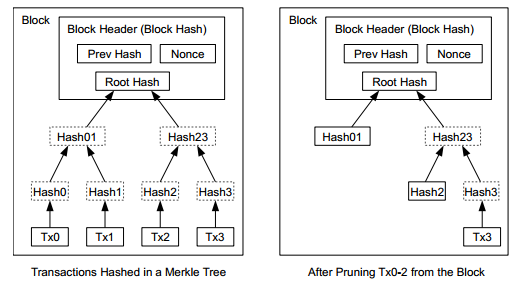
We see that the entire Bitcoin transaction history is stored in each Bitcoin transaction node. Even if disk space is not a problem now, it will definitely become a problem in the future. Bitcoin uses a Merkle Tree so that transaction nodes can remove part of the transaction history at any time while maintaining the integrity of the entire chain.
As shown in the left figure below, each transaction calculates a hash value, these hash values are paired two by two to calculate a hash value, and then paired two by two… until the root hash is calculated. Each node in the tree either contains original transaction information, a hash value, or both child nodes exist. In this way, we can delete any selected original transaction information at any time to save disk space. The right figure below is the Merkle Tree after deleting transactions 0, 1, and 2. In extreme cases, we can delete all original transaction information and only leave the Root Hash.
If all transaction information is trimmed, a block header is 80 bytes. Calculated at a speed of one block every 10 minutes, this chain will only grow by 4.2MB per year, which is not a problem at all.
Scalability
VISA processes approximately 2000 transactions per second, and can process 10000 transactions per second during peak periods. Until the end of 2012, the Bitcoin network processed an average of 0.5 transactions per second. [6]
Each transaction requires approximately 0.2KB ~ 1KB, calculated at an average of 0.5KB [6], to process 2000 transactions per second, requires 7.8Mbps bandwidth, which is naturally nothing for servers. Therefore, in terms of network communication, Bitcoin can easily support VISA scale.
A Core i7 CPU core can do 8000 digital signature checks per second, and each transaction requires an average of two digital signature checks (each transaction has an average of two inputs [6], each input requires a digital signature check), that is, a single-core CPU can process 4000 transactions per second, reaching VISA scale.
Therefore, as a transaction system, the scalability of Bitcoin is not a problem. But if you want to use Bitcoin’s longest chain algorithm for other types of network services, you may need to consider scalability issues, and it is best to reduce the number of messages broadcast across the entire network.
Controlled Bitcoin Issuance
After all this, we haven’t talked about where Bitcoin comes from. One of the clever designs of Bitcoin is that the “one CPU one vote” mechanism that protects the transaction history is also the mechanism for issuing Bitcoin. Every time a difficult problem is solved, that is, a block is calculated, a certain number of Bitcoins can be obtained (note, not one Bitcoin). This makes it so that in the early stages of Bitcoin development and for a long time afterwards, people will invest a lot of computing power to “mine” in order to get Bitcoin rewards. The more people mine, the stronger the computing power, and the harder it is for those trying to tamper with history to succeed.
In order to control the issuance of currency, Bitcoin rewards are decreasing. At the beginning (2009), you could get 50 bitcoins for each block mined. From 2009 to 2013, a total of 10.5 million bitcoins were issued, accounting for 50% of the total issuance of Bitcoin. After 210,000 blocks, that is, from 2013, the reward was halved, that is, 25 bitcoins could be obtained for each block mined. From 2013 to 2017, a total of 5.25 million bitcoins were issued, accounting for 25% of the total. After that, the reward will be halved approximately every four years (rounded down to the nearest 1 satoshi), until the year 2140, when the reward for each block mined will drop from 1 satoshi (1/100M Bitcoin) to 0, and all 21M bitcoins will be issued, and no more bitcoins will be available.
Some people may ask, we mine and get 0.1, 0.01 bitcoins, and never get 25 bitcoins? That’s because mining alone is too difficult. Getting 25 bitcoins is considerable, but given the current difficulty, it takes an average of 1.1259018e+19 attempts to find a block (the difficulty increases by 30% every 11 days on average!). Therefore, mining alone is high-risk, and generally, people join mining pools. The mining pool internally distributes tasks, shares risks and rewards, turning the luck-based activity into a stable investment where Bitcoin income is basically proportional to computing power. Some mining pools distribute the bitcoins mined (25 at a time) evenly according to the computing power invested by the participants; some mining pools settle according to the invested computing power regardless of whether bitcoins are mined or not.
In fact, if Bitcoin’s difficulty control (retarget) works as expected, 90% of bitcoins will be issued in 2018, and 99% of bitcoins will be issued in 2030. (The number of bitcoins expected to be issued each year: Link) Decades later, if Bitcoin is still in circulation, people may invest computing power not for mining, but to protect transaction history. In the world of Bitcoin, transaction history is everything, so Bitcoin holders will invest computing power to protect their wealth.
The fact that Bitcoin has become the first popular electronic currency in human history is inseparable from its clever algorithm design. If the design of distributed systems can be inspired by Bitcoin, it would be a great benefit.
Reference Answers
- How to verify a Bitcoin transaction so that it is undeniable? Based on open key cryptography digital signature.
- How to avoid spending a Bitcoin twice? Longest chain, one CPU one vote, transaction history is completely open.
- If I alone have 10% of the network’s computing power, is it possible to rewrite history? It is almost impossible to rewrite history more than an hour ago.
- Why do Bitcoin transactions have to wait for tens of minutes? To generate enough subsequent blocks to ensure that transactions are not tampered with in a probabilistic sense.
- How does Bitcoin ensure a limited quantity (21 million)? Every 210,000 blocks, the reward for each block produced is halved, so the issuance of Bitcoin changes over time as a geometric sequence.
- How to ensure that a Bitcoin is mined exactly every 10 minutes? The question is not phrased correctly, it’s not about mining a Bitcoin, but mining a block. And it can’t be guaranteed, it’s just through the dynamic adjustment of difficulty (retarget), that the network produces a block approximately every 10 minutes.
- How does one mine 0.1 Bitcoin at a time? Joined a mining pool, rewards are shared.
- Does a transaction of 10,000 bitcoins require generating 10,000 transaction information? No, Bitcoin can be merged.
- With such a large volume of Bitcoin transactions, how are transaction records transmitted and stored? Transaction history can be trimmed, network bandwidth and CPU required to verify digital signatures are not currently bottlenecks.
References
- https://bitcoin.org/bitcoin.pdf
- Bitcoin wiki: https://en.bitcoin.it/wiki/Category:Technical
- Bruce Schneier, “Applied Cryptography: Protocols, algorithms and source code in C” (Second Edition)
- W. Diffie and M. E. Hellman, “New Directions in Cryptography”, IEEE Transactions on Information Theory, 1976
- http://bitcoin.sipa.be/
- https://en.bitcoin.it/wiki/Scalability
- https://en.bitcoin.it/wiki/Controlled_Currency_Supply